Factors and Factoring Expressions

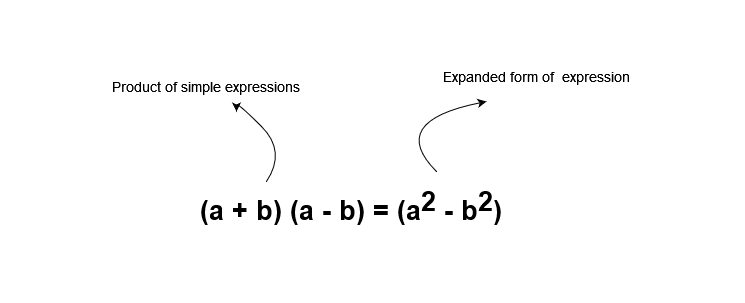
In the previous lesson, you learned about distributive law and how to use them to rewrite expressions. The distribution law applied on factored expression and it changes into distributed form. The factored form of expression is showing the function as a product of two simpler expressions which when multiplied will be in expanded form.

In this article, I am going to talk about factors and factoring expressions. I assume that you know about expression, if not then you can read previous lessons of this course.

Factors

All numbers are expressions, called numeric expressions or simply constants. There are two types of numeric constants – prime numbers and composite numbers. The prime numbers have only two factors – 1 and itself. If a is prime number , then its factors are 1 and a. Other numbers which are composite numbers, have more factors including 1 and the number itself.

What are factors of a number ?

To understand factors let’s take an example number – .

Let’s make a list of all numbers that divide perfectly which means if you divide by those numbers you selected , you get as remainder. I have listed then below.

\begin{aligned}\bf 1, 12, 6, 2, 4, 3\end{aligned}

These are factors of number . If we multiply these numbers ,we get . For example, and and and multiply to give us .

Let us now try to find factors of a prime number. For example, we can find factors of number . You will note that number has no other divisor than and itself , therefore, its factors are and . This is a prime number.

Prime Factorization

Every number is multiple of prime numbers and the number 1 is factor of all numbers. To find all prime numbers that are factors of a number is called prime factorization.

For example,

We can divide number by which is prime factor. We get 6 as quotient, the number is divisible by , which gives as quotient. We divide by and the quotient is . Therefore, by prime factorization, our factors are or you can write . We only count prime numbers and leave and which are also factors of .

Greatest Common Factor

Sometimes you want to compare two numbers and find a greatest factor that are common to both number. It is called greatest common factor or GCF. We can find GCF of two numbers by listing all known factors of a number or by prime factorization method.

For example,
To find the greatest common factor of number and using the factor listing method.

List all factors of : which is: .
List all factors of : which is:

The number is the greatest common number and hence, it is the GCF of and . You can find the GCF of more than two numbers without any problem using the same method.

Let us, find the GCF through prime factorization method.

We take two number which is 10 and 25 again.

If we divide 10 with prime numbers only, we get.

5 and 2 as prime factors.

If we divide 25 with prime numbers only we get,

5 because 25 is square of 5.

Once again the common factor is 5 which is the greatest common factor for 10 and 25.

Factoring expressions

An expression is made of terms and each term is made of coefficient and variables. By taking common factors, we are breaking the expression into simple expressions and show it as product of those simple expressions. Factors multiply to give the expanded form of expression. So we separate greatest common factors from each term, the negative sign, and least common multiples of variables during the process of factorization.

Steps to find the the factors of an expression is:

1. Find the greatest common factor of coefficients of expression.
2. Find out if sign of factor is negative or positive.
3. Least common multiples of variables
4. Write down the factors as product of simple expressions.

Let us see few examples to understand this better. But, before that you must understand few terms about expressions.

An expression with single term is called a monomial. for example,

is a monomial
is a monomial.

An expression with two terms is called a binomial and expression with three term is called a trinomial. An expression made of several monomial is called a polynomial. All expression with one or more terms is essentially a polynomial.

Example 1:

Write the following monomial in factored form:

Step 1:

The first step is to find the GCF for the coefficient 6.To find the coefficient of , we use prime factorization method and list out all prime factors for .The prime factors of are:

Step 2:

Second step is to, check if the term is negative, if yes, then our factor is negative. otherwise , it is positive only. Always check the first term only. The first term decides whether GCF is a positive or a negative number. Suppose is a monomial then first term is negative which is a negative value.

Step 3:

The third step, find the variables and their multiples. The variables are letters such as or any letter from English alphabets.Here we have variable raised to which means variable ‘x’ multiplied to itself times.

Now , We can write out expression in factored form as

multiplied by and if you multiply them, you get . This of course, is a verbal expression. We could write it as

\begin{aligned} \bf(2x^2) \dot (3x) = 6x^3\end{aligned}

Example #2

Write the following expression in factored form:

First step is to find the factors of coefficients of both terms using prime factorization method.

has factor .
has factors
The greatest common factor is .

Step 2:

The second step is to check the sign, the greatest common factor is negative because the first term of the expression is negative. For example, the first term has a negative coefficient . Therefore, the greatest common factor is also negative.

Step 3:

The third step is to find the least common multiple for variables.

First term has multiplied times.
Second term has multiplied by .

multiplied is least common multiple. Therefore, our factors are multiplied by . We must be careful about signs because negative multiplied by negative is positive value.

Summary

Let summarize that you learned in this lesson. To find the factors of an expression, you must do the following

1. Find the GCF or greatest common factor for all terms in the expression.
2. If the first term is negative then the factor is also negative.
3. List out the least common multiple for variables.
4. Write down your expression as a product of simple expressions.