Introduction To Sets

In this article, I will introduce you to sets and its notations. There are many definitions for sets. But no one single definition is acceptable. So, I will start with a simple informal definition of a set.

“A set is group of objects with some properties and sometimes the object from same group does not share same properties”.

Advertisements

Suppose is a set of students from a school. Students in school are a in a set, but all students do not study same course. Some study math and other study programming and so on. In other words, they have different properties.

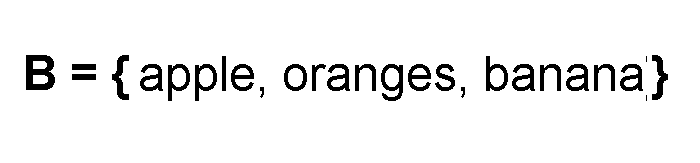
Let be a set of fruits: it has and all fruits have different taste and color.

What is the definition of set?

The formal definition of a set is:

A set is an unordered collection of objects called its members or elements. A set contains elements or members.

Here unordered is important and we will come back to it later. If an element belongs to a set, then we write which means element ‘a’ is in set A.

If an element does not belong to a set, we write which means that element ‘a’ is not in set A.

Set Notations

There are two ways to describe a set.

• Roster notation
• Set builder notation.

Roster notation

In roster method, you simply list all the elements of a set within braces. If is a set of soft drinks, then list all the elements inside curly braces, separated with a comma. You have already seen an example above.

The roster method works when you have limited elements in a set. In other words you can count the number of elements in a set.

Set Builder Notation

When the size of set is too large, and you are not able to list the element, use the set builder notation. You are simple creating a rule for the elements of a set.

For example:

Suppose is set of all numbers less than , then you write this in set builder notation within curly braces like this.

A = {x \in N \mid x < 100}

Note that we wrote as a set, not because is set of natural numbers from which we got elements of . Sometimes elements of a set come from a bigger group called its Universe.