In the previous lesson, you learned about Cartesian coordinate system, graph of equations and linear equations. These are prerequisites to learn about function in this lesson.
A function is a relation between two sets – set A and set B, where each element 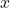
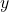
The elements 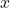
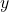
Rules for Function
A function must follow certain rules, otherwise it is not a function.
- Every element of set A must be assigned to an element of set B.
- Each element of set A must match with an element in set B.
- An element of set B can be output of two or more elements of set A.
- An element of set A cannot be input of two or more elements of set A. (See rule 2).
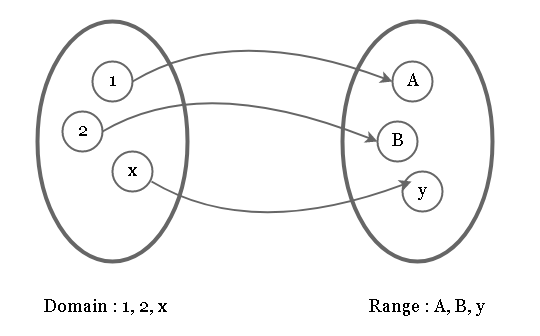
What are the different ways to represent functions ?
There are 3 ways to represent functions.
Numerically – you can represent a function as set of ordered pairs (x, y) where x is the domain of the function and y is the range of the function.
For example, you can represent above diagram as
{(1, A), (2, B), (x, y)}Algebraically – you can represent a function using algebraic notations. A function is denoted as 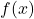
For example, you are given an expression 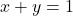
The above expression can be changed to following form
y = 1 - x
or
f (x) = 1 - x
Graphically – you can represent a function using graph. A reveal lot of information about function such a increasing function, decreasing function, odd or even and other characteristics.
To represent a function using graph find the points required to plot the graph of the function. This is done using algebraic expression of the graph.
For example, let’s draw the graph of
| x | f (x) | points (x, (f (x)) |
| -1 | 2 | (-1, 2) |
| 0 | 1 | (0, 1) |
| 1 | 0 | (1, 0) |
| 2 | -1 | (2, -1) |
The graph of the function using above points is given below.
Piecewise-Defined Functions
A domain of a function is all real numbers. Sometimes a function is piecewise-defined. It means there are more than one function for different values of domain.
You need to specify two or more equations to represent a function with specific domain values.
For example,
f(x) = x2-1x<0x -1x≥0
Points to Remember
- If x value falls under the domain, then the function f(x) is defined for x and if x does not falls under the domain of f(x) then it is undefined for x.
- When the domain of the function is not mentioned then the implied domain is set of all real numbers.
- The range of the function must be a possible value after inserting x into the function f (x). The range falls between