The bisection method is a root finding numerical method. Given a function the bisection method finds the real roots of the function. In this article you will learn to write a program for bisection method.
Problem Definition
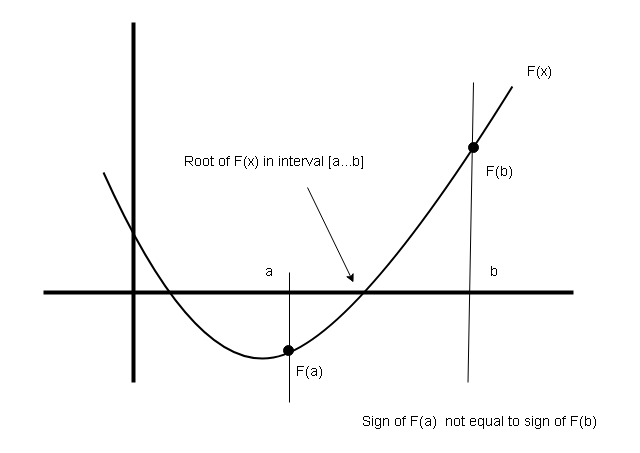
The bisection method find the real roots of a function. Suppose you are given a function 
Read More: Bisection Method
The value
- The sign of
sign of
.
- The function
- Cuts the interval into 2 halves and continue searching smaller half for roots.
- Keep cutting the interval into smaller and smaller halves until interval is too small.
- The final value at the smallest interval is the root.
Program Code – Bisection Method
/* C++ Program to evaluate a function using Bisection Method
Function: F(x) = x^3-4x-9
File Name: BisectionMethod.CPP
Author: NotesforMSc
*/
#include "iostream.h"
#include "stdio.h"
#include "conio.h"
#include "math.h"
#define MAX 20
void main()
{
int i;
double a, b, m,fa,fm;
//Initialize variables
fa = fm = 0.0;
m = 0.0;
clrscr();
cout << "\n\t Enter initial value:";
cin >> a;
cout << a << endl;
cin >> b;
cout << b << endl;
cout << "\n\n\t\t SOLUTION BY BISECTION METHOD"<< endl;
// Bisection Method
i = 1;
while(i < MAX)
{
m = (a + b)/2.0;
fa = (a * a * a) - 4 * a - 9;
fm = (m * m * m) - 4 * m - 9;
//Check the smaller intercal
if(fa < 0 && fm > 0) {
b = m;
}
else {
a = m;
}
i++;
}
//Print the Results
cout << "\n\t Result";
cout << "\n\t Root is" << " " << m << endl;
getch();
}
Output – Bisection Method
Enter Initial Value: 2
2
3
3
SOLUTION BY BISECTION METHOD
Result
Root is 2.70653
References:-
Shun Yan Cheung () The Bisection Method, Available at: http://www.mathcs.emory.edu/~cheung/Courses/170/Syllabus/07/bisection.html (Accessed: 6/19/2019).
University of Waterloo, Department of Electrical and Computer Engineering () Topic 10.1: Bisection Method (Examples), Available at: https://ece.uwaterloo.ca/~dwharder/NumericalAnalysis/10RootFinding/bisection/examples.html (Accessed: 6.119/2019).