C++ Program for Factorial without Recursion

• Previous
• Next

Factorial of a number is the number you get by multiplying all the numbers up to that number including the number itself. The program for factorial does not use a programming technique called a recursion. a recursion happens when a function calls itself until the problem is solved.

This program is a simple computation of factorial value, hence, it is suitable for beginner learners of C++ programming. I have written this using Dev-C++ compiler version 4.9.9.2 installed on a windows 7 64-bit system.

Problem Definition

The program requires user input – a positive integer value and computes the factorial of than number.

For example,

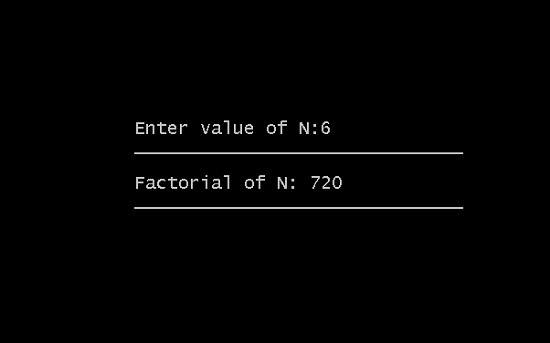
Suppose you entered number 6 , then the factorial of this number would be

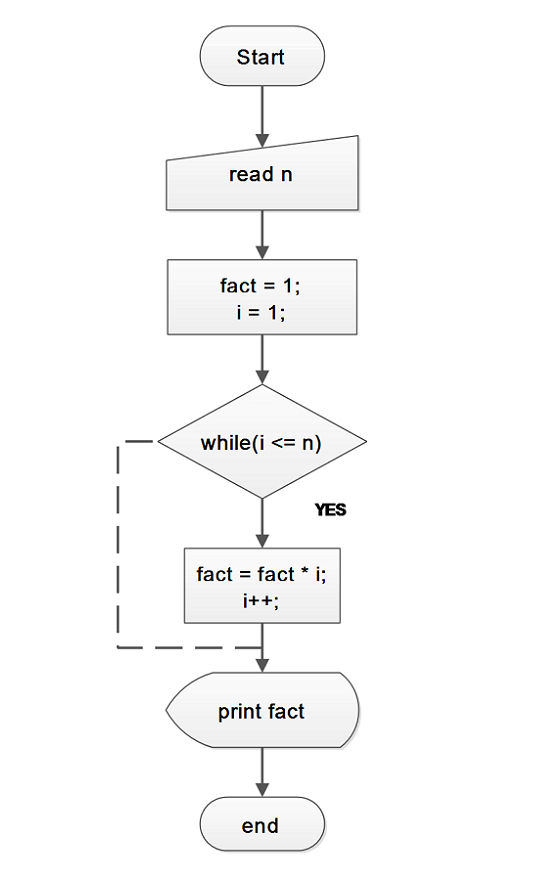
1 x 2 x 3 x 4 x 5 x 6 = 720

In mathematical terms, if n is a positive integer value, the factorial of n is denoted by n! You can go through the flowchart to understand the logic of factorial applied in this program.

Flowchart – Factorial without Recursion

Program Code – Factorial without Recursion

// Program to compute factorial of n numbers

#include <iostream.h>
#include <stdlib.h>
#include <stdio.h>

int main()
{

    int fact,i;

    int n;

//Read the value of N

    cout << "Enter value of N:" ; cin >> n;

//Initialize Factorial to 1 and i to 1

    fact = 1;

    i = 1;

    while(i<=n)
    {

        fact = fact * i;

        i++;

    }

// Print the value of factorial

    for(i=0;i < 30;i++)
    cout << "_";cout << "\n\n";

    cout << "Factorial of N:" << "\t" << fact << endl;

    for(i=0;i << 30;i++)
    cout << "_";cout << "\n\n";

    system("PAUSE");

    return 0;

}

Output

---

• Previous
• Next