Rewriting Expressions using Distributive Law

Table of Contents

In the previous article, you learned about rewriting expressions using commutative law, associative law and sometimes with identity law.The expressions are sometimes presented in the form of product of simple expressions, and we can expand it my multiplying those expressions. One such method is distribution of multiplication over addition or subtraction. In this article, I am going to discuss about distributive law and how to rewrite expressions using distributive law.

Distributive Law.

The distributive law is a special mathematical property, also called distributive property that distributes multiplication over addition or subtraction. The distributive law is written as a (b + c) is equal to ab + ac where a, b and c are some real numbers. Real numbers are all numbers that you can think of, except some special numbers called the complex numbers. In future lessons, you will learn about real numbers, but for now let’s focus on distributive law.

\begin{aligned} &a(b + c) = ab + ac \\\\ &where \\\\ &a, b, c \in \mathbb{R} \end{aligned}

Distributive Law for Subtraction

The distributive law for subtraction is a(b – c) equal to ab – ac. It is similar to distributive law for addition.

\begin{aligned} &a(b - c) = ab - ac \\\\ &where \\\\ &a, b, c \in \mathbb{R} \end{aligned}

Each of the number inside the parentheses are multiplied with variable a which means multiplication with a is distributed to each variable inside of the parentheses.

Distributive Law – watch on YouTube

How to we know if distributive law is correct?

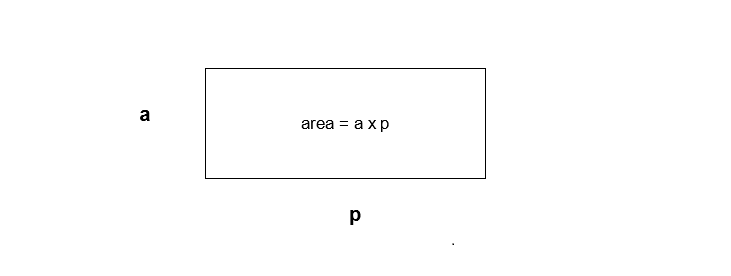
Suppose there is a rectangle with length a and width p. To find the area of this rectangle we must multiply a with p, meaning $area = length \times width$ . This is our original rectangle.

Figure 1 - Area = length x width which is a x p — Figure 1 – *Area = length x width* which is *a x p*

Now, divide the rectangle into two by dividing the width p into b and c. The area of rectangle is still length x width, but we write it as

\begin{aligned} &area = a(b + c) \\\\ &where \\\\ &(b + c) = p \end{aligned}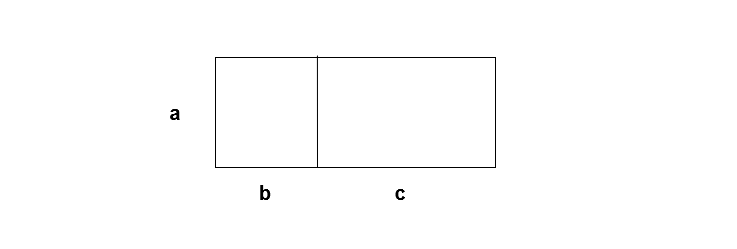

Figure 2 - The original rectangle is split into two with p = b + c — Figure 2 – The original rectangle is split into two with p = b + c

We can observe that there are two smaller rectangles with width = b and width = c. If we combine the area of smaller rectangles we can find the area of the original rectangle.

\begin{aligned} &Area \hspace{3px} first \hspace{3px} rectangle = a \times b\\\\ &Area \hspace{3px} second\hspace{3px} rectangle = a \times c\\\\ &Therefore, a(b + c) = ab + ac = Area \hspace{3px} of \hspace{3px} original \hspace{3px} rectangle \end{aligned}

Let distributive law be $a(b + c) = ab + ac$ . Suppose $a = 5$ , replacing a in the equation, we get

5(b + c) = 5b + 5c

It is same as $ab + ac$ .

Distributive law for Subtraction.

The distribution law for subtraction is similar to distributive law for addition.It is in the form:

a( b - c) = ab - ac

Let’s try to understand this with an example.

Example #1:

Rewrite the following expression using distributive law.

\begin{aligned} &4(a + b)\\\\ &by \hspace{3 px} distributive \hspace{3 px} law, \hspace{3 px}x(a + b ) = xa + xb\\\\ &Therefore, \hspace{3px}our \hspace{3px}we\hspace{3px} know\hspace{3px} that \hspace{3px}x = 4,\\\\ &Replacing \hspace{3px}x \hspace{3px}with \hspace{3px}4, \hspace{3px}we \hspace{3px}get \hspace{3px}4a + 4b \hspace{3px}as \hspace{3px}answer. \end{aligned}

Example #2:

Rewrite the following expression using distributive law

\begin{aligned} &2(5x - 1)\\\\ &Expression \hspace{3px} in\hspace{3px} form:\\\\ &\hspace{3px} a(b - c) = ab - ac.\\\\ &2( 5x ) - 2 (1)\\\\ &we \hspace{3px} get , \hspace{3px} 10x - 2\\\\ \end{aligned}

For variables with a coefficient, you can multiply the coefficient with any number. Here we multiplied coefficient $5$ with $2$ to get $10x$ .

Now, sightly difficult problem,

Example #3:

Rewrite the following expression using distributive law.

\begin{aligned} &3(2x - 3y)\\\\ & \end{aligned}

In this expression, we have two variables and their own coefficients. But, that will not stop you from applying distributive law. Remove the parenthesis and our expression becomes

\begin{aligned} &(3 \times 2x) - (3 \times 3y)\\\\ &6x - 9y \end{aligned}

$6x - 9y$ is the expanded form of the expression 3(2x – 3y)$ after applying distributive law.

Summary

You learned about distributive law and how to rewrite expression in expanded form by applying the distributive law. The distributive law is distribution of multiplication over addition or subtraction which simplify the expression. Sometimes you are given expanded for of expression and ask to write them as factored form. It is done by taking common factors from the expression. In the next lesson, we shall see how this is done.