A binary tree is a special kind of tree and important in computer science. There is plenty of real-world application of binary trees. The scope of this lesson is limited to the learning the binary tree concepts.
Informal definition
A tree is called a binary tree if it has the following properties.
- It is an empty tree with no nodes.
- The tree has a root node, left sub-tree and right sub-tree.
- The sub-trees are binary tree themselves.
Strictly Binary Tree
Suppose there is a binary tree with right sub-tree and left sub-tree. The sub-trees are in turn non-empty, then such a binary tree is called a strictly binary tree.
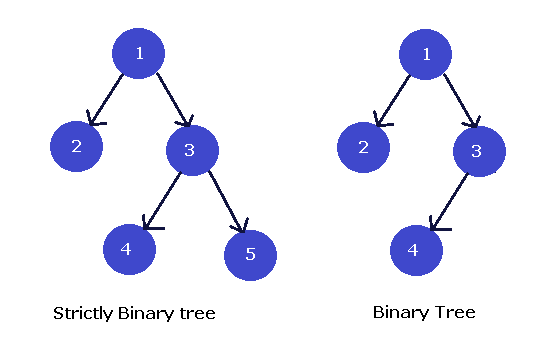
In the above figure, one is a strictly binary tree and the second tree is not a strictly binary tree, but it is certainly a binary tree and satisfy all the properties of a binary tree.
Complete Binary Tree
A complete binary tree has a level L and all its leaf nodes are available at level L. At each level the complete binary tree contains 2Lnodes.
Let us show this with an example,
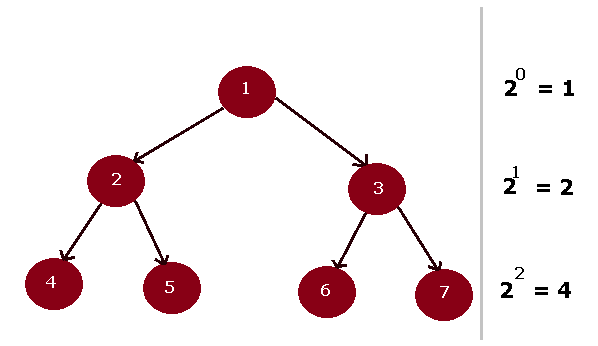
The root is at level 0, therefore, L = 0 and 2^L = 2^0 = 1.
Conversion of a Binary Forest into a Binary Tree
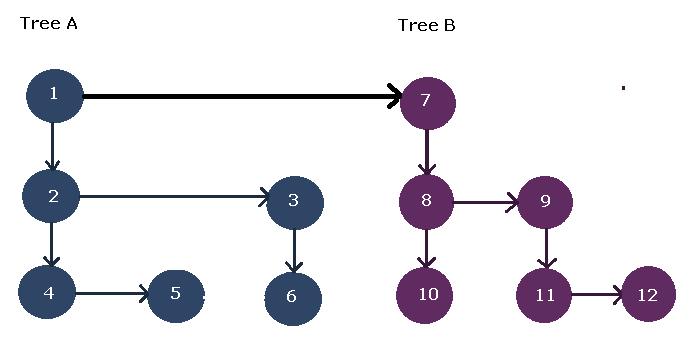
Suppose we have a forest with two trees as follows,
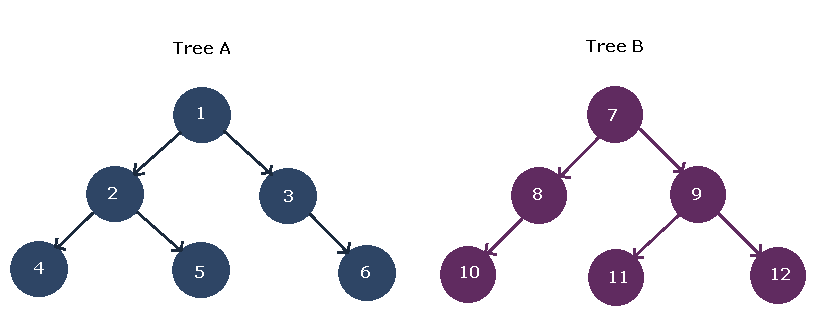
\begin{aligned}
&T1 = { 1,2,3,4,5,6}\\
&T2 = { 7,8,9,10,11,12}
\end{aligned}The figure below show the two separate trees in the forest.
The first step is to order the nodes of both trees using following formula.
- If a node has left child, then if comes immediately below the node.
- If a node has another node in the save level, then it becomes the right child of the node.
- If a node has right child then, ignore it.
Such a representation of two trees is given below.
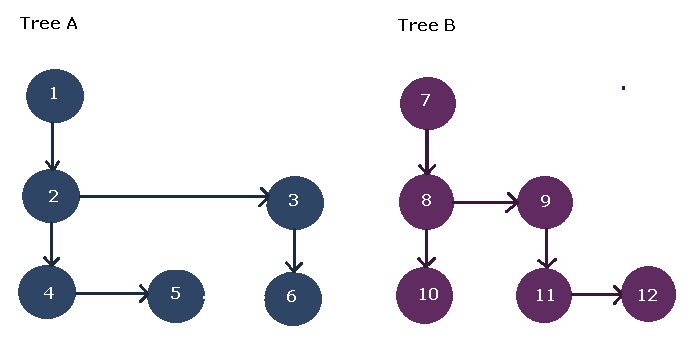
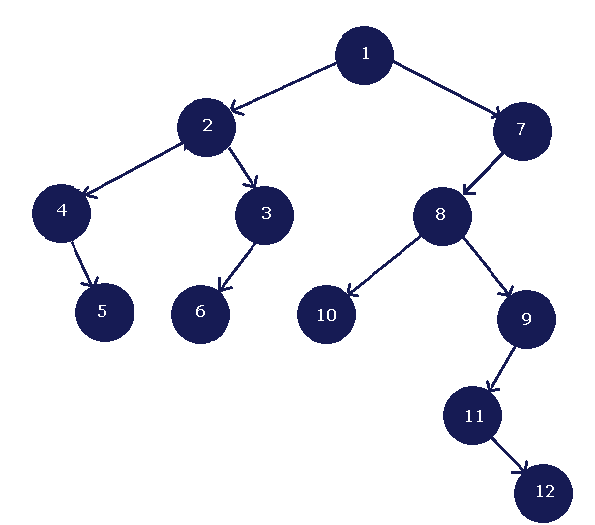
Your next step should be to join these two tree into one by connecting their roots. This is because the roots of the trees are at the same level. See the figure below
The new tree is a binary tree, the node at the save level in above diagram becomes the right child. The final tree structure look like the one in figure below.
Total Number of Edges
In a complete binary tree, the total number of edges is given by the formula,
\begin{aligned}
2 (N_L - 1)\hspace{1ex} where \hspace{1ex}N_L\hspace{1ex} is \hspace{1ex}total\hspace{1ex} number \hspace{1ex}of\hspace{1ex} leaf \hspace{1ex}nodes.
\end{aligned}For example, see the tree below.
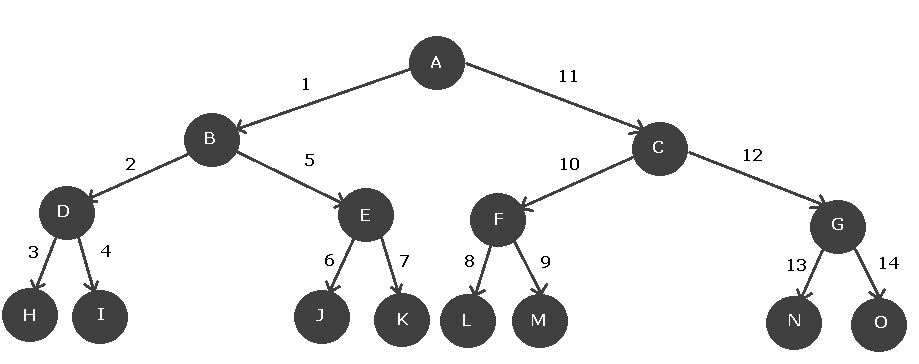
In the above diagram, we have ![]() .
.
Therefore,
\begin{aligned}
&= 2( N_L - 1) \\
&= 2 ( 8 - 1) \\
&= 2 (7) \\
&= 14\hspace{1ex} edges.
\end{aligned}Height of a Binary Tree
The maximum level of any node of the binary tree is called the height of a binary tree.
For example, see the figure below.
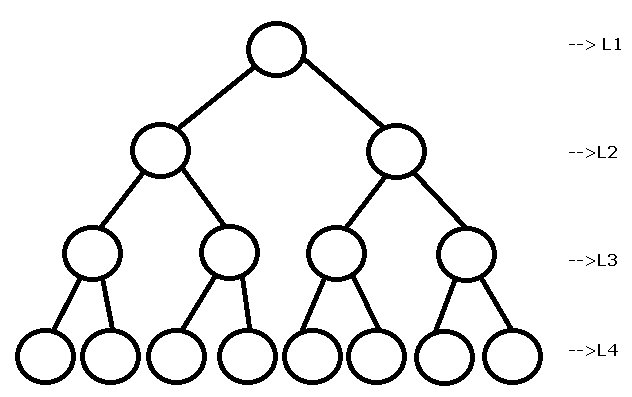
In the above tree figure, the maximum level of the tree is ![]() ,
,
Therefore, the height of the tree is ![]() .
.
References
R.G.Dromey. 2008. How to Solve it by Computer. Pearson Education India.
Robert Kruse, Cl Tondo. n.d. Data Structures and Program Design in C. Pearson Education India.
Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein. 2009. Introduction to Algorithms. MIT Press.