A tree is a non-linear data structure. It means you cannot access an element of a tree in a straightforward manner. In this lesson, you learn about tree basics.
This will serve as a foundation for future topics on trees. You can start learning about other topics if familiar with the basics.
Informal definition of Tree
A tree is a set of one or more nodes with a special node called a Root node. Every none points to a left node and a right node. Sometimes left, right or both are missing and a node points to nothing.
Every node is part of some smaller set of nodes called a Sub-tree. Each sub-tree has more sub-trees.

Tree basics – Directed vs Undirected Tree
In an undirected tree, the edge between two nodes has no direction associated with it. However, a directed tree has some important properties.
- The directed tree is acyclic means there is loop between the nodes.
- The directed tree is digraph means it is like a graph with direction. Each node has associated edges. If the node pointed by some other node, it is called an In-degree and if the node is pointing to some other node, its called an Out-degree.
- Root node has in-degree 0 and all other nodes have in-degree of 1.
- The minimum number of nodes allowed in a directed tree is 1. So, an isolated node is a directed tree.
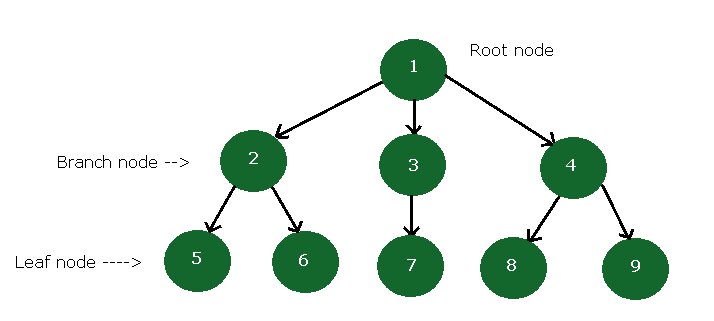
Leaf Nodes
In a directed tree with nodes that has an out-degree of 0 is called a Leaf node or Terminal node.
In the above figure, 5, 6, 7, 8, 9 are leaf nodes.
Branch Nodes
In a directed tree with all nodes other than root and leaf nodes are called Branch nodes. For example,
In the above figure, 2, 3 and 4 are branch nodes.
Level of a Tree
Suppose you want to reach the node 8 from root node 1, then starting from root node, we go through following path
1 –> 4 –> 8
So, the level of any node is length of its path from the root node. The level of root node is 0 and level of node 8 is 2.
Tree basics – Ordered Tree
Sometimes the directed tree is ordered, that is, at each level the order is specified, and this type of tree is called an Ordered tree.
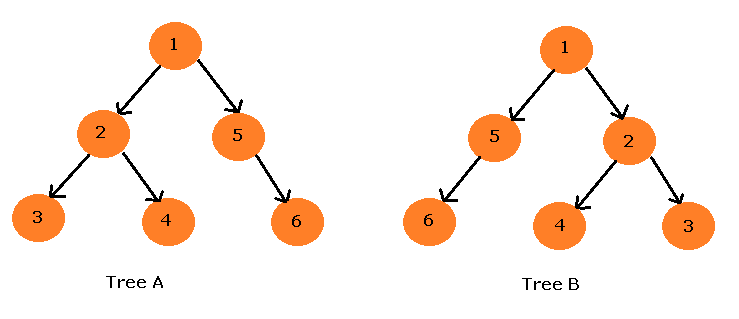
In the above figure, the Tree A and Tree B are the same tree but ordered differently.
Node degree
The node degree corresponds to number of children of the node. The node 3,4,and 6 in tree A are leaf nodes and has a degree of 0 because it not a parent of any other node.
The node 2 from tree B has a degree of 2 because node 4 and node 3 are its children.
The Concept of Forest
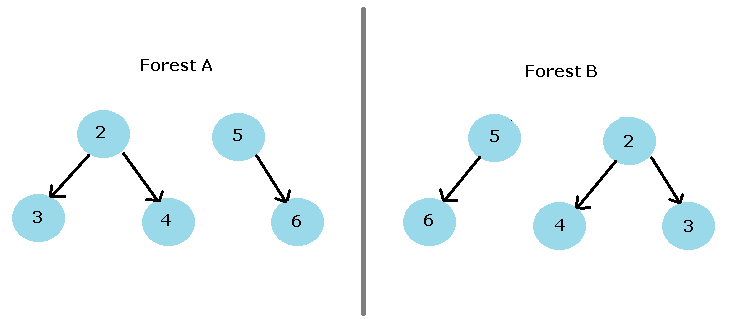
If we delete root node and its edges from tree A or tree B, we will get two separate trees. This particular set of trees is known as a Forest.
For example, we get the following forest after deleting the root. These forest can be represented as sets.They are the same sets.
Forest A ={ (2,3,4),( 5,6)} Forest B = {(5,6),(2,3,4)}
Descendant and Children of a Node
There is a node called S and it is reachable from node N means there is a path from N to S. Then an such node S is called a Descendant of a node N.
Suppose a node S reachable by a single edge E from node N is called a Child of node N and the node N is a Parent of child node S.
For example, In Tree A
The node 2 and node 5 are children of node 1
The node 3 and node 4 are not children, but descendant of node 1.
Note: We will be using this tree basics terminology in all future lessons. Make yourselves familiar with the concepts.
References
E.Balaguruswamy. 2013. Data Structures Using C. McGraw Hill Education.
Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein. 2009. Introduction to Algorithms. MIT Press.
