Now we know the concept of a binary tree – both ordered and unordered, the height, level, node concept and leaf node. If have not learned any of these, visit following links. In this lesson, you will learn about binary tree operations.
- Data Structure – Tree Basics.
- Data Structure – Binary Tree Concepts
- Data Structure – Difference between Ordered Tree and Unordered Tree
A data structure store data in a particular manner and applications perform some operation after retrieving those data.In order to fetch the data, the application must perform some operations on the data structure. Also, it must conform to the rules of the data structure and perform other those operations that are allowed.
Tree Representation
Before discussing the operations, you must understand how a binary tree is represented using a programming language.
There are many ways to represent a tree data structure, but we will not talk about them now. The most common representation is using a linked-list. The linked-list representation of a binary tree is given below.
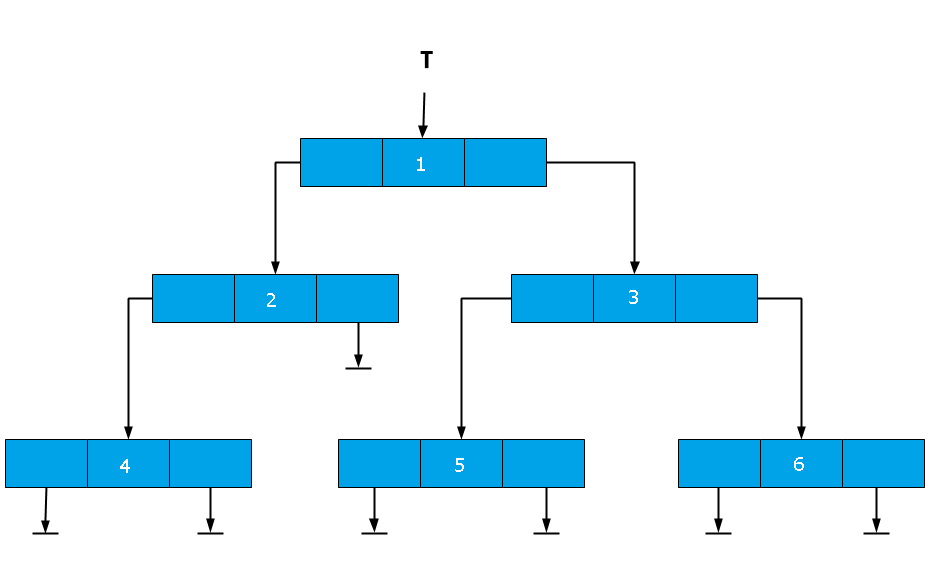
Each node in the tree is connected to its left child and right child using a link-pointer and some of the node including the leaf node the link-pointer points to nothing or null.
Binary Tree Operations
There are many common operations performed on a binary tree – insert a node, delete a node, update a node data and traversing the tree structure to search for a particular node.
Traversal of a Binary Tree
Since a tree is not a linear structure, so traversing tree is difficult because we want to go through each node only once, giving the impression of a linear search.
There are 3 ways to traverse a binary tree.
- Pre-order traversal
- In-order traversal
- Post-order traversal
Preorder Traversal (Root -> Left -> Right)
The steps to traverse the binary tree in preorder method is given below.
1. Process the root
The preorder traversal starts from the root node and process(Print) the root node data.
2. Traverse the left sub-tree in preorder
After traversing the root node, preorder method traverse the left sub-tree. Now the left sub-tree is the root of its own sub-tree, so preorder method is applied once again, that is, process the root and look for left sub-tree again and so on.
This means preorder traversal method goes all the way to left until no more left sub-tree is available.
3. Traverse the right sub-tree in preorder
When there is no left node available, the preorder traversal process the right sub-tree. The node in the right sub-tree becomes the root and left node is empty, so it traverses all the right sub-tree until all are processed successfully.
Example – Preorder Traversal (Binary Tree Operations)
The following binary tree is traversed using a preorder traversal method and the result is printed.
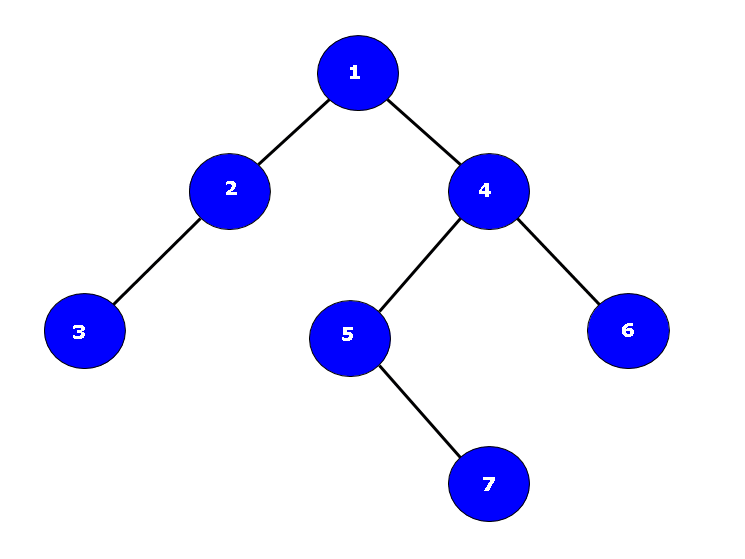
To do a preorder traversal we need to start at root level;
Preorder iteration 1:
Print the root – node 1
go to left sub-tree – node 2
Preorder iteration 2:
print the new root – node 2
go to left sub-tree – node 3
Preorder iteration 3:
print the new root – node 3
go to left sub-tree – no node
go to right sub-tree – no node
Now we have printed node 1, node 2 and node 3 whose left sub-tree is already explored. We must check the right sub-tree in preorder method.
Preorder iteration 5:
print the new root – node 4
go to left sub-tree – node 5
Preorder iteration 6:
Print the new root – node 5
Go to the left sub-tree – no node
Go to the right sub-tree – node 7
Now, node 4, node 5 and node 7 are printed and node 6 is remaining whose parent is node 4.
Preorder iteration 7:
Print the new root – node 7
Go to the left sub-tree – no node
Go to the right sub-tree – no node
Preorder iteration 8:
Print the new root – node 6
No left
No right
Final Preorder Sequence:- 1 -> 2 -> 3 -> 4 -> 5 -> 7 -> 6
Inorder traversal (Left –>Root –> Right)
The steps to traverse the binary tree in an in-order traversal method is as follows.
1. Traverse the left sub-tree of root in an in-order
The in-order traversal starts from the left sub-tree of a root node and keep traversing until no left node available because every time a left node is encountered, it must do the in-order traversal once again.
2. Process the root node
After the left traversal is over and no more left node available, it must process(Print) the root node.
3. Traverse the right sub-tree in an in-order
When the root is printed and the left node is traversed, the in-order traversal, process the right sub-tree. The node in the right sub-tree is traversed until no more is remaining.
Example: – In-order Traversal (Binary Tree Operations)
Consider the same diagram above, an in-order traversal sequence is given below.
To do an in-order traversal we need to start at a root level, but we will move quickly to left sub-tree and then print the root and move to right sub-tree. Every time left sub-tree is exhausted, immediately print the root and explore the right sub-tree.
In-order iteration 1:
The root – node 1
Go to left sub-tree of root – node 2
In-order iteration 2:
Root is now node 2
Go to left sub-tree – node 3
In-order iteration 3:
Root is now – node 3
Go to left sub-tree – no node
Print the root – node 3
Go to the right sub-tree – no node
Now we check the node above it – node 2 because left sub-tree of the node 2 is completely taken care of.
In-order iteration 4:
Print the root – node 2
Go to right sub-tree – no node
Now check the node above it – node 1 because left sub-tree of node 1 is completely traversed and we already processed node 3 and node 2.
In-order iteration 5:
Print the root – node 1
Go to left sub-tree – no node
Go to right sub-tree – node 4
In-order iteration 6:
The new root – node 4
Go to left sub-tree – node 5
It has no left sub-tree so print the node 5.
In-order iteration 7:
The new root – node 7
No left
No right
Print the node 7 and the left sub-tree of node 4 is now complete.
Inorder iteration 8:
Print the root – node 4
No left
Go to the right sub-tree – node 6
We print the node 6 because there is no left sub-tree or right sub-tree.
Final Inorder Sequence:- 3 -> 2 -> 1 -> 5 -> 7 -> 4 -> 6
Post-order traversal ( Left –>Right –> Root)
The steps to traverse the binary tree in an in-order traversal method is as follows.
1. Traverse the left sub-tree of root in an post-order
The post-order traversal also starts from the left sub-tree of a root node like in-order traversal and keep traversing until no left node available because every time a left node is encountered, it must do the post-order traversal once again repeatedly.
2. Traverse the right sub-tree in post-order
After the left traversal is over and no more left node available, it moves to the right sub-tree of the node and continue to traverse in post-order method.
3. Process the root node
When all the left nodes and right nodes are traversed, the post-order traversal, process the root node.
Example: – Post-order Traversal (Binary Tree Operations)
Consider the same diagram above that we have been using so far, a post-order traversal sequence is given below. For a post-order traversal we start at root level, but we will move to left sub-tree and move to right sub-tree. Every time left sub-tree and right sub-tree is exhausted, immediately print the root.
Post-order iteration 1:
The root – node 1
Go to left sub-tree of root – node 2
Post-order iteration 2:
Root is now node 2
Go to left sub-tree – node 3
Post-order iteration 3:
Root is now – node 3
Go to left sub-tree – no node
Go to the right sub-tree – no node
Print the root – node 3
Now we check right sub-tree the node above it – node 2 because left sub-tree of the node 2 is completely taken care of.
Post-order iteration 4:
Back to root – node 2
Go to the right sub-tree – no node
Print the root – node 2
Now check the node above it – node 1 because left sub-tree of node 1 is completely traversed.
Post-order iteration 5:
Back the root – node 1
Go to right sub-tree – node 4
Post-order iteration 6:
The new root – node 4
Go to left sub-tree – node 5
Post-order iteration 7:
The new root – node 5
No left
Go to the right sub-tree.
Post-order iteration 8:
Print the root – node 7
No left
No right
Print the root – node 7
Now the right and left sub-tree of node 5 is complete.
Post-order iteration 9:
Back to the root – node 5
Left sub-tree – done
Right sub-tree – done
Print the root – node 5
The node above node 5 is node 4 whose left sub-tree is now complete, we then go to the right sub-tree.
Post-order iteration 10:
Back to the root – node 4
Left sub-tree – done.
Go to the right sub-tree – node 6
post-order iteration 11:
New root – node 6
No left
No right
Print the root – node 6
Now we go back to the node above it which node 4, the right and left of the node 4 is done.
Post-order iteration 12:
Back to the root – node 4
Left sub-tree – done
Right sub-tree – done
Print the root – node 4
Finally, the right and left sub-tree of the node 1 is done, so we print the node 1 at the end.
Final post-order Sequence:- 3 -> 2 -> 7 -> 5 -> 6 -> 4 -> 1
These are the binary tree operations – traversal. In the next lesson, you will learn about other binary tree operations like inserting a node and deleting a node from binary trees.
References
R.G.Dromey. 2008. How to Solve it by Computer. Pearson Education India.
Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein. 2009. Introduction to Algorithms. MIT Press.