How to create a Hasse Diagram

Table of Contents

Hasse Diagram is created for POSET or Partially Ordered Set. It means that there is a set of elements in which certain element are ordered, sequenced or arranged in some way. It is usually denoted as ≤, this is not “Less than, Equal to”, this symbol shows that elements are ordered.

Now, there is a relation among all the elements in the partial order set and it is some binary relation R, this relation must satisfy following properties

Reflexive
Anti-Symmetric
Transitive

Example Problem

Suppose (z, |) is a partial order set where | is division operator and a | b means “a divides b”.

Reflexive Property

a | a => a divides itself and this is correct with respect to division. A number can divide itself.

Anti-Symmetric Property

a | b = b | a is correct and works only when a = b. If not, then it is not anti-symmetric.

Transitive Property

a | b => a divides b means b = a * m where m is some number. (1)

b | c => b divides c means c = b * n where n is some number. (2)

Using (1) and (2) we get

c = (a * m) * n

c = a * (m * n) which is same as (1). This proves the transitivity property.

Hasse Diagram

Now that we know partial order set means and a Hasse Diagram is graphical representation of posets.

Rules for Hasse Diagram

If x < y, then in the graph x appears lower to y.
We draw line segment between x and y only if x cover y or y cover x, it means some order is maintained between them.

Consider an example

Let A be a set, A = { 1, 3, 5, 12, 15 }, relation between elements are a | b that is., a divides b.

Step 1

Due to the reflexive property all elements have direct edge to itself.

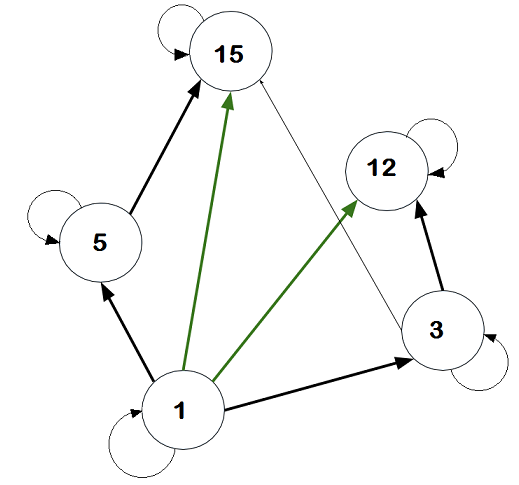
In this diagram, it shows the relations removed all the self-directing loops.

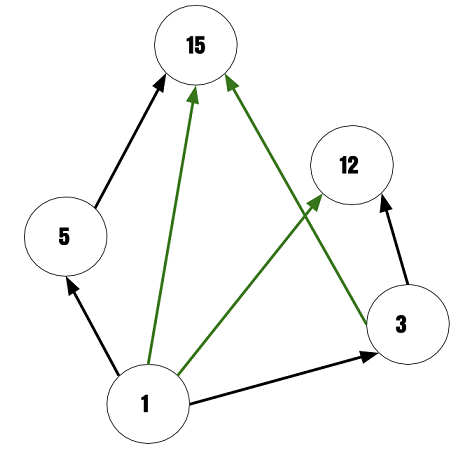
Step 2

The green lines shows transitivity, so we remove all the transitive lines. Out diagram look like the following.

Hasse Diagram without Transition and Loops

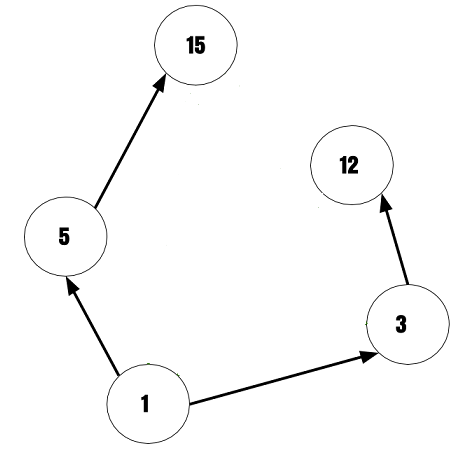
Step 3

Replace all the vertices with dots and directed edges with ordinary lines. This final diagram is called the Hasse Diagram of poset.

Hasse Diagram for A = { 1, 3, 5, 12, 15 } and relation a | b i.e., a divides b

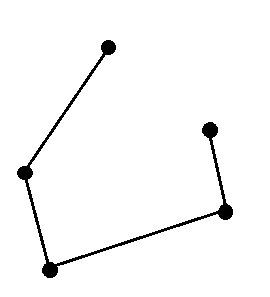
Exercise

Here is an exercise for you to practice. The prerequisite for Hasse Diagram is to know how to represent relations using graphs.

Let A be a poset, A = { 2, 4, 6, 8 } and the relation a | b is ‘a divides b. Draw a Hasse Diagram for the poset showing all the relations.