Logical Connectives and Truth Tables

Table of Contents

Logical statements have truth values such as true or false. One or more simple logical statements can be connected to make a compound statement which also has truth value. The connectives are logical operators that connect one or more logical statements or atomic statements.

Advertisements

The outcome depends on the truth value of individual statements that are part of the compound statement; therefore, all combination of truth values for each atomic statements displayed in a tabular form called the truth table including outcome for each input combinations.

In prepositional logic, there are 5 basic logical connectives which is the topic of this article. These are,

Connective	Name	Symbol
Negation	Not operator	$\neg$
Conjunction	And operator	$\land$
Disjunction	Or operator	$\lor$
Implication	if-then operator	$\implies$
Biconditional	if-and-only-iff or iff	$\iff$

List of basic logical connectives

Negation ( $\neg$ )

We have already discussed negation in previous video. Negation simply negates the truth value of an atomic statement. If $p$ is a statement with value – True, then $\neg p$ is False.

The truth table for negation is given below.

$\textbf{p}$	$\neg \textbf{p}$
$T$	$F$
$F$	$T$

Truth table for negation

Conjunction (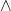 $\land$ )

The conjunction is connective that takes two or more atomic statements and make a compound statement. The output of conjunction is similar to boolean and operator. If all the input combination of a compound statement is True, then the output is True; otherwise, it is False. The conjunction or and operator works on the “all or nothing” principle. The truth table for conjunction is given below.

$\textbf{p}$	$\textbf{q}$	$\textbf{p} \land \textbf{q}$
$T$	$T$	$T$
$T$	$F$	$F$
$F$	$T$	$F$
$F$	$F$	$F$

Truth table for conjunction

The total number of rows in this table depends on the number of variables; therefore, if there are two variables.

Number \hspace{5px} of \hspace{5px} rows = 2^n = 2^2 =4

Note that the only row with result True is where both inputs are True.

Disjunction (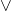 $\lor$ )

The disjunction is similar to boolean OR logic. It takes one or more atomic statement and makes a compound statement. If the said compound statement is True then there is at-least one atomic statement with a truth value – True. The truth table for disjunction also depends on the number of variables.

$\textbf{p}$	$\textbf{q}$	$\textbf{ p} \lor \textbf{q}$
$T$	$T$	$T$
$T$	$F$	$T$
$F$	$T$	$T$
$F$	$F$	$F$

Truth table for disjunction

In the next article, we will discuss about the implication and biconditional connectives. We discuss why they are different from other basic connectives.

Negation ()

Conjunction ()

Disjunction ()

Ads Blocker Detected!!!

Negation ( $\neg$ )

Conjunction ( $\land$ )

Disjunction ( $\lor$ )