Discrete Math - Prepositional Logic

Table of Contents

We know that the simple statements are represented as p, q and so on. Suppose we are given a compound preposition.

$p \land q$

There is another property of compound prepositions called the duality; Therefore, the dual of above statement is

$p \lor q$

The dual can be achieved by interchanging $\land$ by $\lor$ or interchanging $\lor$ by $\land$ . This means $\land$ and $\lor$ is dual of each other.

Dual For Another Type Of Statement

We will see an example of another type of prepositional statement in which we use True or False directly instead of a variable.

For example,



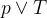is a preposition with T or True as one of the variable.

The dual of such a statement can be obtained by interchanging $\lor$ by $\land$ and interchanging True with False or False with True.

Each of the statement can be derived from the other.

Understanding Duality Using Truth Tables

These are the truth tables for the statements – $p \land q$ and $p \lor q$ .

If we change the operator for $p \land q$ with $p \lor q$ , or vice-versa, we get dual of each other. The truth table validates this claim. We can check this for other prepositional statements also.

$p$	$q$	$p \land q$
T	T	T
T	F	F
F	T	F
F	F	F

$p$	$q$	$p \lor q$
T	T	T
T	F	T
F	T	T
F	F	F

Prepositional Logic – Duality

Dual For Another Type Of Statement

Understanding Duality Using Truth Tables