Prepositional Logic-Implication and Biconditional

Table of Contents

In the previous video, you learned about different types of basic logical connectives that helps in creating compound prepositions. These connectives are join two or more atomic statements to form compound preposition which also have a truth value of its own.

We have discuss negation, conjunction, and disjunction connectives so far, the remaining two connectives are discussed in this article.

Implication ( $\implies$)

The implication connective takes one or more variables that represent atomic statements and make a compound statement. The implication is denoted with the $\implies$ symbol which means “implies” or “if…then..”.

In programming world, if-then is popularly known as conditional statement.

For example, Let $ p$ and $q$ be two atomic statements.

\begin{aligned} &p: "Today\hspace{3px} is\hspace{3px} Sunday."\\\\ &q: "I\hspace{3px} don't \hspace{3px} go\hspace{3px} to\hspace{3px} school."\\\\ &Then,\hspace{3px} p \implies q \hspace{3px} is \hspace{3px} "if \hspace{3px} p,\hspace{3px} then\hspace{3px} q" \hspace{3px} or \hspace{3px} "p \hspace{3px} implies \hspace{3px} q", \\\\ &p \implies q: \hspace{3px} "If\hspace{3px} today\hspace{3px} is \hspace{3px} Sunday, \hspace{3px} then \hspace{3px} I \hspace{3px} don't \hspace{3px} go \hspace{3px} to \hspace{3px} school" \end{aligned}

The statement $p$ is called antecedent or premise and the statement $q$ is called consequent or conclusion.

Other English Phrases That Represent If…Then..

There are several other ways to write implication in English, some of them are

q, if p
q, provided that p
q unless p
q follows from p
p sufficient condition or q
q necessary condition for p
because p, q
p therefore q

Translating English sentences to logic statements with variables may be tricky because there could be several meaning to same statement and we are not asserting a particular truth value to statement $p$ or $q$ .

It means that we are not saying that $p$ is true so that we have $q$ ; therefore, we want material implication which is weak and tentative in nature.

This could be understood with the help of truth table of implication.

Suppose $p$ is “You study hard” and $q$ stands for “You will pass the exam”. The $p\implies q$ is “If you study hard, then you will pass the exam”.

Let say $p$ is true, and $q$ is true as well, then $p \implies q$ is true. Similarly, $p$ is true and $q$ is false.

For the row 3 and row 4, we could not use $p \implies q$ as false because the table will look like truth table for $p \land q$ .

Biconditional Operator ( $p \iff q$ )

The biconditional connective also takes one of more atomic statements and create a compound statement that has a truth value of its own. The biconditional is an “if and only if” or “iff” statement. The biconditional operator is denoted by $\iff$ .

For example if  and 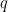 are two logical atomic statements.

: "I am hungry" 

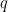: "I worked very hard this morning" 

Then 

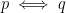 : "I am hungry if and only if I worked very hard this morning"

Here is the truth table for biconditional connective.

From the truth table it is evident that when both the variables have same truth values – true or false. The compound preposition with a biconditional connective is true.

For example, let $p$ be the preposition “It is raining today” and $q$ be the statement “Peter will stay in house”. If both the statement is true, then whole statement is true, else both the statements are false then the statement is false.

The biconditional is implication that true from $p \implies q$ and $q \implies p$ . For example, consider the following statement.

 : "A polygon is a triangle" 

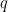 : "A triangle has 3 sides" 

Using the biconditional we can make following statement.

"A polygon is a triangle if and only if it has 3 sides"

Condition for above statement are

If polygon is triangle then it has 3 sides ( $p \implies q$ )
If polygon has 3 sides, then it is a triangle ( $q \implies p$ )

Note that the both conditions we get and equivalent preposition for biconditional.

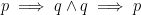
Let us verify the claim using a truth table.

logical equivalence of p<->q = p->q and q->p

From the truth table above, clearly, both expression are logically equal. Whenever you are asked to simplify a compound statements involving biconditionals, replace it with above expression for convenience.

$p$	$q$	$p \implies q$
$T$	$T$	$T$
$T$	$F$	$F$
$F$	$T$	$T ?$
$F$	$F$	$T ?$

$p$	$q$	$\neg p$	$p \implies q$	$\neg p \lor q$
$T$	$T$	$F$	$T$	$T$
$T$	$F$	$F$	$F$	$F$
$F$	$T$	$T$	$T$	$T$
$F$	$F$	$T$	$T$	$T$

$p$	$q$	$p \iff q$
$T$	$T$	$T$
$T$	$F$	$F$
$F$	$T$	$F$
$F$	$F$	$T$

$p$	$q$	$p \implies q$	$q \implies p$	$p \iff q$	$p \implies q \land q \implies p$
$T$	$T$	$T$	$T$	$T$	$T$
$T$	$F$	$F$	$T$	$F$	$F$
$F$	$T$	$T$	$F$	$F$	$F$
$F$	$F$	$T$	$T$	$T$	$T$

Implication ( $\implies$)

Biconditional Operator ( )

Ads Blocker Detected!!!

Biconditional Operator ( $p \iff q$ )