Venn Diagram, Universal Sets, Subsets, and Power Sets

In the previous article, you learned about the basic type of sets and its notations. In this article, I am going to discuss about Venn diagram, and some other types of sets. These sets are different from what I have discussed in my previous post, which was about equal sets, equivalent set and empty sets etc.

Venn Diagrams

Venn diagram is a graphical representation of sets. All sets come from a universe, called the universal set and represented by the letter . This universal set contains all the elements with common attributes
that we want to study.

• population of a country,
• students in a university,

can belong to a universal set, and then we can create sets from the universal set. If students from university belong to our Universal set, then we can have a set of students studying computer science or mathematics. In Venn diagram,

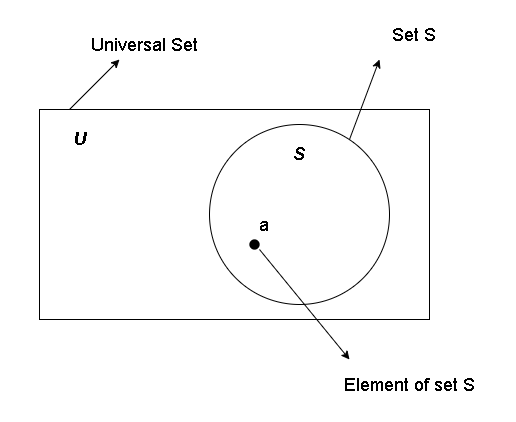
the universal set is a rectangle and sets are circles, that may or may not overlap each other. We will come back to that later.

For example, at the beginning, the elements are part of universal set , and when you make a set then they belong to the set if they have the property to be member of the set.

Example #1

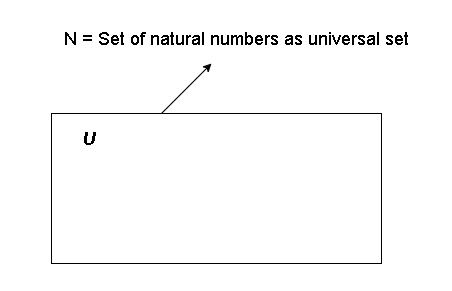
Suppose is the set of natural numbers, and it’s our universe. To show the natural number set using Venn diagram, we will make a rectangle.

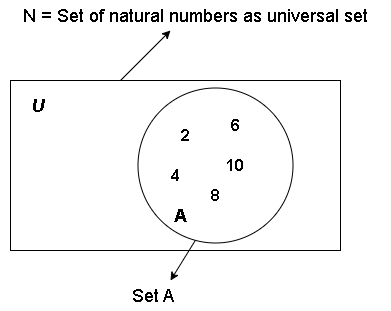
Let be a set of all even numbers less than 11.

\begin{aligned}&A = \{ 2, 4, 6, 8, 10 \}\end{aligned}

We did not add zero because Natural numbers start from 1.

N = \{1,2,3, \cdots \}

Now draw a circle inside the rectangle and show all even numbers within the circle. This is the Venn diagram representation of a set with elements. All numbers that are not shown in circle are in the Uniserve .

Example #2

Let’s take another example, Let and be two sets with elements.

\begin{aligned}
&X = \{ 2, 5, 6\}\\\\
&Y = \{4, 5, 9\}
\end{aligned}

If we construct these two sets using Venn diagram, the circles that represent these two sets are overlapping, it is because they have a common element 5. The elements are shown as dots in Venn diagram.

The Venn diagrams are useful in visualizing the set operations like union, intersection, set difference, etc. We will explore the set operations in future lessons.

Subsets of a Set

Let us talk about subsets. Let there be two sets and .

Definition: The set is subset of set if and only if every single element of set is also an element of set .

We can also write this in equation form.

\begin{aligned}
&A \subseteq B = \forall x\{a \in A \implies x \in B\}\end{aligned}

For sets that are not subsets is denoted as

\begin{aligned} 
&A \nsubseteq B = \forall x\{x \in A \implies x \notin B\}
\end{aligned}

Venn Diagram Representation of Subsets

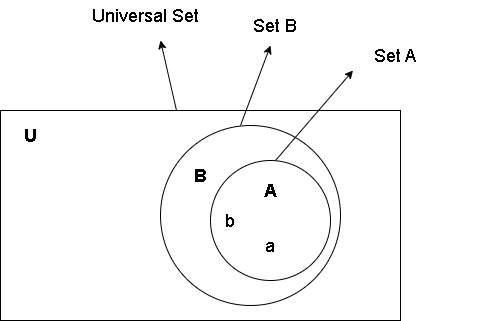
Here is a Venn diagram representation of subset. Since, is subset of , it is inside of the bigger circle representing set .

When we talk of subsets, there is a theorem:

If A is a set, it is guaranteed that it has at least two subsets:

1. Empty set - empty set is subset of all sets.
2. The set itself - the set automatically becomes subset of itself because it is all the elements.

Proving Equal Sets Using Subsets

This brings an interesting problem. If you remember that equal sets are two sets with same elements. If X and Y are two equal sets with same elements. Then we can prove that they are equal if we can show that they are subsets of each other.

So Let A be set of all odd numbers less than 10. and B is set with members { 1, 3, 5, 7}.

First, empty set is member of both sets. Second, all elements in set A are also in set B, and all elements of set B are in set A. Therefore, they are subsets of each other and equal.

Proper Subsets

Now we talk about proper subsets. A is proper subset of B such that all elements of A are in B , but some elements from B are not in A. It can written in logical form as .

“Forall x{ x in A implies that X in B}
and forsome x {x in B and x not in A}”

The proper subset is denoted as A proper subset of B.

Venn Diagram Of Proper Subsets

The Venn diagram of proper subset will look like this, for some set A and B. Now the question comes to our mind. How many subsets can we make from a given set ?

Power Set of a Set

This kind of set which contains only subsets of a set is called its power set. If set A is an ordinary set with 3 elements, then power set of A is denoted as P(A) and the number of subsets in a power set is 2^n. In our case,
set A has 3 elements, therefore, it has 2^3 = 8 subsets.

The power set of set A look like this and it has two guaranteed subsets, empty set and itself as members.

Disjoint Sets

Two sets that are not related at all, it means they don’t have any common elements are called the disjoint sets.
It is opposite of subsets. If we drew the venn diagram of disjoint set, then it will look like two separete circles away from each other. It is because their elements are different.

Super Sets

Finally, let us talk about supersets. If set A has all the elements of set B then set A is super set of set B.” It is denoted as A super set of B.

Proper super set is when A is super set of B, but A is not equal to B, there are some elements that are only available in set A.

Let A be a finite set with elements { 1, 3, 8, 7, 4} and B be set with elements { 3, 7}. Then A is super set of B
because it has all the elements of set B. It is also a proper super set because set A is not equal to set B.

If we draw Venn diagram for set A and set B, it look similar to the Venn diagram of subsets where B is subset of A.

Properties of Super Sets

Here are some properties of super sets.

1. Every set is a super set of empty set because empty set has no elements in it. Also empty set is member of every set.
2. If B is subset of A, it means that A is the super set of set B. Therefore, we can say that super sets are opposite of subsets. This is the reason, their Venn diagram look similar, however, set description is different.

Summary

Let us review things you learnt in this article.

1. First you learnt the basics of Venn diagram and know how to represent sets and universal sets.
2. Next you have understood the universal set as bigger set from which you get other sets.
3. You learnt about subset that contains elements from other set.
4. You know about proper subsets which are similar to subsets but contains less elements that its super sets.
5. Power set is a set of subsets
6. disjoint sets are two unrelated sets.
7. and finally, super sets that has all the element from its subsets.