Hasse Diagram is created for POSET or Partially Ordered Set. It means that there is a set of elements in which certain element are ordered, sequenced or arranged in some way. It is usually denoted as ≤, this is not “Less than, Equal to”, this symbol shows that elements are ordered.
Now, there is a relation among all the elements in the partial order set and it is some binary relation R, this relation must satisfy following properties
- Reflexive
- Anti-Symmetric
- Transitive
Example Problem
Reflexive Property
Anti-Symmetric Property
Transitive Property
Hasse Diagram
Rules for Hasse Diagram
- If x < y, then in the graph x appears lower to y.
- We draw line segment between x and y only if x cover y or y cover x, it means some order is maintained between them.
Step 1
Due to the reflexive property all elements have direct edge to itself.
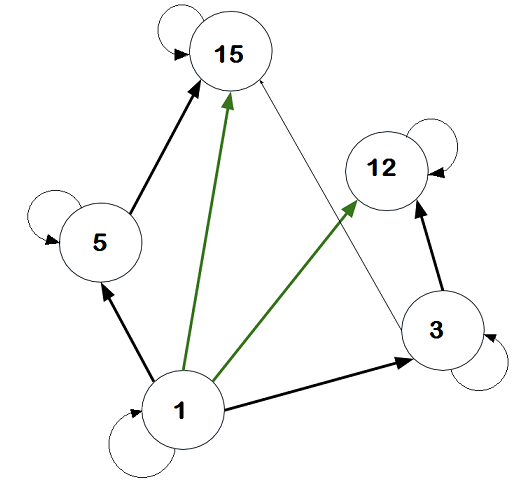
In this diagram, it shows the relations removed all the self-directing loops.
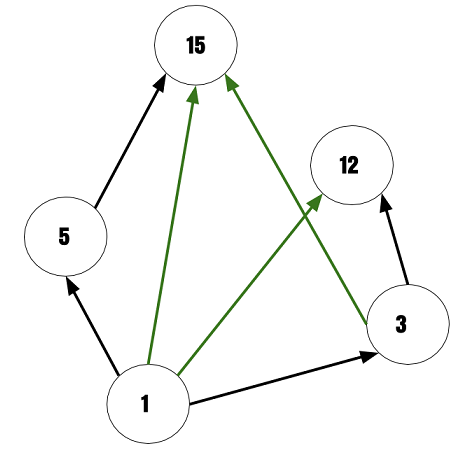
Step 2
The green lines shows transitivity, so we remove all the transitive lines. Out diagram look like the following.
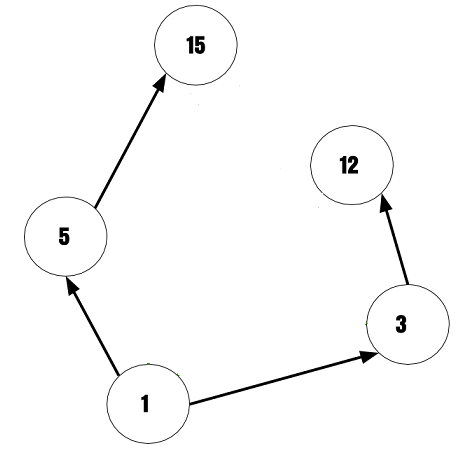
Step 3
Replace all the vertices with dots and directed edges with ordinary lines. This final diagram is called the Hasse Diagram of poset.
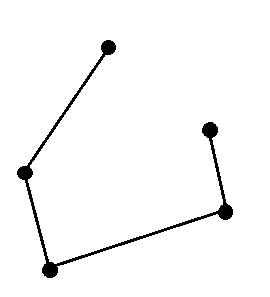
Exercise
Here is an exercise for you to practice. The prerequisite for Hasse Diagram is to know how to represent relations using graphs.
Let A be a poset, A = { 2, 4, 6, 8 } and the relation a | b is ‘a divides b. Draw a Hasse Diagram for the poset showing all the relations.
