Table of Contents
The Fibonacci search algorithm is another variant of binary search based on divide and conquer technique. The binary search as you may have learned earlier that split the array to be searched, exactly in the middle recursively to search for the key. Fibonacci search on the other hand is bit unusual and uses the Fibonacci sequence or numbers to make a decision tree and search the key.
Like binary search, the Fibonacci search also work on sorted array ( non-decreasing order).
The Fibonacci Sequence
Simply said the Fibonacci sequence is a set of numbers where any term $latex F_n&s=1$ is equal to the sum of previous two terms.
F_{n} = F_{n-1} + F_{n-2}If we try to generate first few terms of a Fibonacci sequence then we get the following numbers.
\begin{aligned}
&F_{0} = 0\\
&F_{1} = 1\\
&F_{2} = F_{1} + F_{0} = 1 + 0 = 1\\
&F_{3} = F_{2} + F_{1} = 1 + 1 = 2\\
&F_{4} = F_{3} + F_{2} = 2 + 1 = 3\\
&F_{5} = F_{4} + F_{3} = 3 + 2 = 5\\
&F_{6} = F_{5} + F_{4} = 5 + 3 = 8\\
&F_{7} = F_{6} + F_{5} = 8 + 5 = 13\\
&F_{8} = F_{7} + F_{6} = 13 + 8 = 21
\end{aligned}Therefore, the Fibonacci sequence is as follows:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34,...
Fibonacci Search
Algorithm Fibonacci_Search(A, n, key)
{
low:= 0
high:= n - 1
loc:= -1
flag:= 0
while(flag != 1 && low <= high)
{
// get the fibonacci f[m-1] < n
index:=get_fibonacci(n)
if ( key == A[index + low]) then
{
flag:= 1
loc:= index
break
}
else if ( key > A[index + low] ) then
{
//adjust the low
low:= low + index + 1
}
else
{
//adjust the high
high:= low + index - 1
}
//adjust the n
n:= high - low + 1
} // end of while
//return success or not
if ( flag = 1) then
{
return (loc + first + 1 )
}
else
{
return -1
}
} //end
Algorithm Fibonacci(n)
{
fibk2:= 0
fibk1:= 1
fibk:= 0
if ( n = 0 || n = 1) then
return 0
while ( fibk <n)
{
fibk:= fibk2 + fibk1
fibk2:= fibk1
fibk1:= fibk
}
return fibk2;
}How Fibonacci Search Works?
Fibonacci search uses the Fibonacci numbers to create a search tree. These are the steps taken during Fibonacci search.
Step 1:
The first step is to find a Fibonacci number that is greater than or equal to the size of the array in which we are searching for the key.
Suppose the size of the array is $latex n&s=1$ and fibonacci number is $latex F_{k}&s=2$.
We must find a $latex F_{k}&s=2$ such that
$latex F_{k} \geq n&s=2$
if $latex n = 10&s=2$ then we must find a $latex F_{k} \geq n&s=2$.
The Fibonacci sequence is
\begin{aligned}0, 1, 1, 2, 3, 5, 8, 13, ...\end{aligned}Therefore, $latex F_{k} = 13&s=2$ because $latex 13 \geq 10&s=2$.
Step 2:
The next step is to compare the key with the element at Fibonacci number $latex F_{k-1}&s=2$.
We know that $latex F_{k} = 13&s=2$ because $latex 13 \geq 10&s=2$. We must find the $latex F_{k-1} &s=2$.
Once again we look at the Fibonacci sequence is
\begin{aligned} 0, 1, 1, 2, 3, 5, 8, 13, ...\end{aligned}Since,
$latex F_{k} = F_{k-1} + F_{k-2}&s=2$
$latex 13 = 8 + 5&s=2$
$latex F_{k-1} = 8 &s=2$
Step 3:
If the key and array element at $latex F_{k-1}&s=2$ are equal then the key is at $latex F_{k-1} + 1&s=2$.
For example, we are searching within an array of 10 elements.
\begin{aligned}&10\hspace{3ex}34\hspace{3ex}39\hspace{3ex}45\hspace{3ex}53\hspace{3ex}58\hspace{3ex}66\hspace{3ex}75\hspace{3ex}83\hspace{3ex}88\\ \\
&A[0]\hspace{1ex} A[1] \hspace{1ex} A[2] \hspace{1ex} A[3] \hspace{1ex} A[4] \hspace{1ex} A[5] \hspace{1ex}A [6] \hspace{1ex} A[7] \hspace{1ex} A[8] \hspace{1ex} A[9]\end{aligned}$latex n = 10&s=2$ and $latex F_{k} = 13&s=2$
Let $latex key = 83&s=2$ and $latex F_{k-1} = 8&s=2$
Therefore, key == A[8] is true.
Then the key is found at $latex F_{k-1} + 1&s=2$ which is $latex 8 + 1 = 9^{th}&s=2$ position.
Step 4:
If the key is less than array element at $latex F_{k-1}&s=2$, then search the left sub-tree to $latex F_{k-1}&s=2$.
For example, we are searching within an array of 10 elements.
\begin{aligned}
&10\hspace{3ex}34\hspace{3ex}39\hspace{3ex}45\hspace{3ex}53\hspace{3ex}58\hspace{3ex}66\hspace{3ex}75\hspace{3ex}83\hspace{3ex}88\\ \\
&A[0] \hspace{1ex} A[1]\hspace{1ex} A[2] \hspace{1ex} A[3] \hspace{1ex} A[4]\hspace{1ex} A[5] \hspace{1ex} A[6] \hspace{1ex} A[7]\hspace{1ex} A[8] \hspace{1ex} A[9]\end{aligned}$latex n = 10&s=2$ and $latex F_{k} = 13&s=2$
Let $latex key = 39&s=2$ and $latex F_{k-1} = 8&s=2$
If key < A[8] is true,
Then search A[0:7] = { 10, 34, 39, 45, 53, 58, 66, 75 }
Step 5:
If the given key is greater than the array element at $latex F_{k-1}&s=2$, then search the right sub-tree to $latex F_{k-1}&s=2$.
\begin{aligned} &10\hspace{3ex}34\hspace{3ex}39\hspace{3ex}45\hspace{3ex}53\hspace{3ex}58\hspace{3ex}66\hspace{3ex}75\hspace{3ex}83\hspace{3ex}88\\\\
&A[0]\hspace{1ex} A[1] \hspace{1ex} A[2] \hspace{1ex} A[3] \hspace{1ex} A[4] \hspace{1ex} A[5] \hspace{1ex} A[6] \hspace{1ex} A[7] \hspace{1ex} A[8] \hspace{1ex} A[9]\end{aligned}$latex n = 10&s=2$ and $latex F_{k} = 13&s=2$
Let $latex key = 83&s=2$ and $latex F_{k-1} = 8&s=2$
If key > A[8] is true,
Then search A[9:9] = { 88 }
Step 6:
If the key is not found, repeat the step step 1 to step 5 as long as $latex F_{k-1} = 0&s=2$, that is, Fibonacci number >= n. After each iteration the size of array $latex n&s=1$ is reduced.
Fibonacci Search Example
In this example, we will take a sorted array and find the search key with the array using Fibonacci search technique. Each iteration will show you the state of lower index, higher index and current value of size n, and Fibonacci number used to locate the key.
Consider the following sorted (non-decreasing) array with 10 elements.
Iteration 1
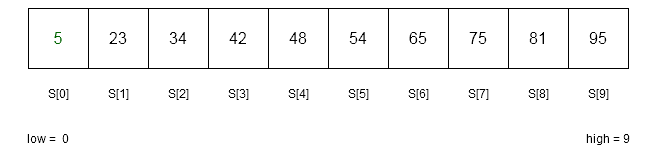
There are 10 elements in the above sorted array S. Therefore,
low = 0
n = 10
high = n-1 = 9
index = get_fibonacci(n) = 8 //because F_{k} = 13
loc = -1 //currect location of the key is outside array
flag = 0 //check whether key is found or not , flag = 1 indicates it is found
key = 65 // we are trying to find 65 in the array
is key == S[ index + low] ?
65 == 81 => NO
is key > S [ index + low] ?
65 > 81 => NO
is key < S[ index + low ] ?
65 < 81 =>YES
high = low + index - 1 // adjust the higher index and keep the low = 0
high = 0 + 8 - 1 = 7
n = high - low + 1 // adjust the size of the array
n = 7 - 0 + 1 = 8Iteration 2
![Figure 2- key is less than S[8]. We must search left sub-tree. The array size n is adjusted to 8 elements.](https://notesformsc.org/wp-content/uploads/2020/12/Figure2-Fibonacci-Search-Array.png)
There are 8 elements in the above sorted array S. Therefore,
low = 0
n = 8
high = 7
index = get_fibonacci(n) = 5 //because previous F_{k} = 8
loc = -1 //currect location of the key is outside array
flag = 0 //check whether key is found or not , flag = 1 indicates it is found
key = 65 // we are trying to find 65 in the array
is key == S[ index + low] ?
65 == 54 => NO
is key > S [ index + low] ?
65 > 54 => YES // key is higher than the array element S[5], move to right sub=-tree
low = low + index + 1 // adjust the lower index and keep the high = 7
low = 0 + 5 + 1 = 6
n = high - low + 1 // adjust the size of the array
n = 7 - 6 + 1 = 2Iteration 3
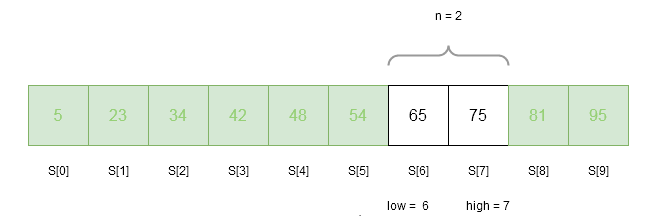
There are 2 elements in the above sorted array S. Therefore,
low = 6
n = 2
high = 7
index = get_fibonacci(n) = 1 //because previous F_{k} = 5
loc = -1 //currect location of the key is outside array
flag = 0 //check whether key is found or not, flag = 1 indicates it is found
key = 65 // we are trying to find 65 in the array
is key == S[ index + low] ?
65 == 75 => NO
is key > S [ index + low] ? // key is higher than the array element S[1], move to right sub=-tree
65 > 75 => NO
is key < S[ index + low ] ? // key is higher than the array element S[1], move to left sub=-tree
65 < 81 =>YES
high = low + index - 1 // adjust the lower index and keep the high = 7
high = 6 + 1 - 1 = 6
n = high - low + 1 // adjust the size of the array
n = 6 - 6 + 1 = 1Iteration 4
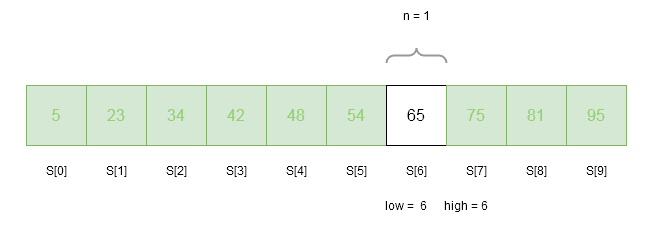
Only 1 element remained in the array, still we must go through the iteration.
low = 6
n = 1
high = 6
index = get_fibonacci(n) = 0 // because when n = 0 or n = 1, simply return 0.
loc = -1 //currect location of the key is outside array
flag = 0 //check whether key is found or not , flag = 1 indicates it is found
key = 65 // we are trying to find 65 in the array
is key == S[ index + low] ? // A[ 6 + 0] = S[6] = 65
65 == 65 => YES
flag = 1
Key is found !Time Complexity of Fibonacci Search
Here is the Fibonacci search decision tree for $latex n=10&s=2$.
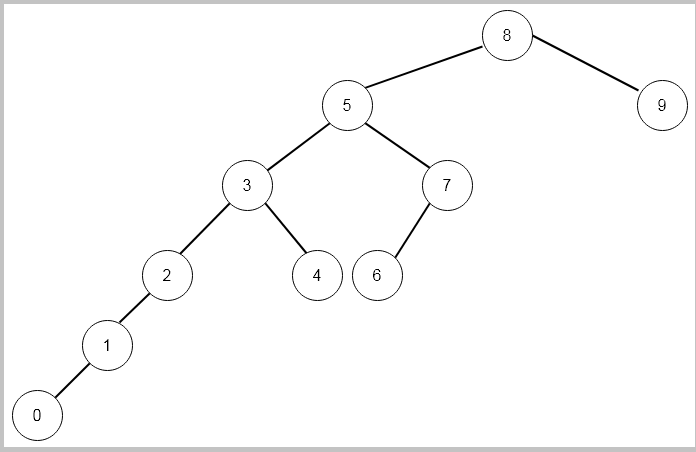
The Fibonacci search also perform like binary search on a sorted array; therefore, the time complexity is in worst case is $latex O( log\hspace{1ex} n)&s=2$.
We can clearly note a few things from the above decision tree.
If the difference in index of grandparents and parent of a node is $latex F_{k}&s=2$ then
- The left sub-tree is of order $latex F_{k-1}&s=2$.
- The left sub-tree is of order $latex F_{k-2}&s=2$.
- This is true for every sub-tree.
- The difference between parent and both children is the same.
- The leftmost path represents a Fibonacci sequence that starts with 0, 1, 2, 3, … .
C++ Implementation Of Fibonacci Search Algorithm
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
int get_fib(int);
int main()
{
int S[10]= { 5, 23, 34, 42, 48, 54, 65, 75, 81, 95 };
int n,key, index, low, high, loc, flag;
n = 10;
low = 0;
int location = -1;
high = n-1;
flag = 0; //Read the key
cout << "Enter Key To Search:";
cin >> key;
index = 0;
while ( flag != 1 && low <= high)
{
index = get_fib(n);
if ( key == S[index + low])
{
location = low + index;
flag = 1;
break;
}
else if( key > S[index + low])
{
low = low + index + 1;
}
else
{
high = low + index -1;
}
n = high - low + 1;
}
if ( flag == 1)
{
cout << "Element Found at Index =" << location << endl;
}
getch();
return 0;
}
int get_fib(int n)
{
int fibk = 0;
int fibk2 = 0;
int fibk1 = 1;
if( n == 0 || n == 1)
{
return 0;
}
while(fibk < n)
{
fibk = fibk1 + fibk2;
fibk2 = fibk1;
fibk1 = fibk;
}
return fibk2;
}Input
Enter Key To Search:65Output
Element Found at Index = 6In the next post, we shall discuss about searching though Hash Table.