The binary search algorithm is very popular search algorithm. It is also known as half-interval search or uniform binary search as it split the array of data into two equal parts recursively until a solution is found. The array in binary search must be sorted.
Binary search employ an algorithm design technique known as divide and conquer. In this technique, a given problem is divided into smaller sub-problems and this is done until no more sub-division is possible.
Then solution to the smallest problem is found and all solutions are combined to get the overall solution to the problem. The divide and conquer technique is not limited to binary search; therefore, we shall discuss this separately in another article.
Binary Search Algorithm
Algorithm Binary Search (S, n , key)
{
low := 0
high = n - 1
while (low <= high)
{
//compute the mid value
mid = low + (high - low)/2
if (key < S[mid]) then
high := mid - 1
else if ( key > S[mid]) then
low := mid + 1
else
return mid
}
}The elements of binary search are as follows.
– The sorted array with data.
– It is the number of elements in the array.
– The search key to be found.
Mid Value
The mid value is most important in binary search as it split the array in to two parts. Then the sub-array is split in the similar way based on divide and conquer technique. The mid is an index of the element in the middle of the array.
mid = low + (high - low)/2How Binary Search Works?
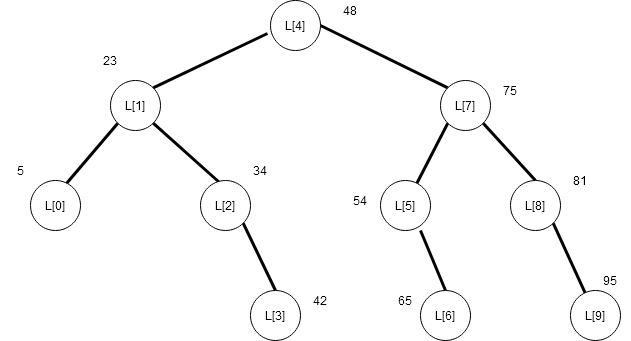
The binary search works on a sorted array. Suppose we have an array with elements in non-decreasing order. To search for a given key, binary search will compute the mid value and thus break the array into equal halves. The key is compared with array element with index value as mid.
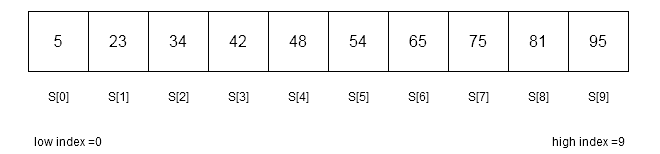
Suppose our is
, then
is calculated as follows.
mid = 0 + ( 9 - 0 ) / 2 = 0 + 4 = 4
//S[4] = 48
//key > S[mid] ( 65 > 48 )
//low = mid + 1
low = 4 + 1 = 5
//low = 5 and high = 9 Now we will consider the upper half of the array for searching with and
.
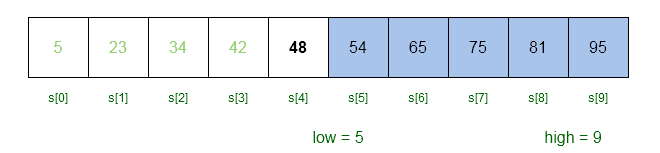
We now have to compute a new mid value in the upper half of the array to search for the key.
mid = 5 + ( 9 - 5 )/2
mid = 5 + 4/2
mid = 5 + 2
mid = 7
//S[7] = 75
//key < S[mid] (65 < 75 )
//high = mid - 1
high = 7 - 1
high = 6
//now, low = 5 and high = 6We will compute the new mid value with and
.
![Figure 3- The old mid is 75 and low = 5 with new high = 6. Our search is limited to S[5] and S[6] only.](https://notesformsc.org/wp-content/uploads/2020/12/Figure3-BinarySearcArray.png)
We only have two element to search for the key. The is calculated using
and
.
mid = 5 + ( 6 - 5 )/2
mid = 5 + 0
mid = 5
//S[5] = 54
//key > S[mid] ( 65 > 54 )
//low = mid + 1
low = 5 + 1
low = 6
//low = 6 and high = 6 The high and low are equal which will be last iteration of while loop in the binary search algorithm. However, is still calculated for the last iteration.
mid = 6 + ( 6 - 6 )/2
mid = 6 + 0
mid = 6
//key == S[mid] ( 65 == 65 )
//mid is returned 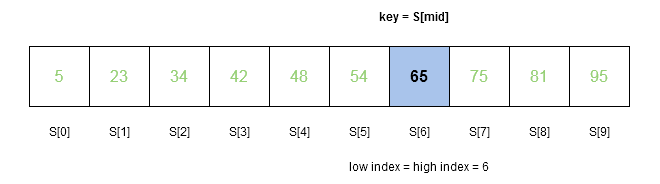
Time Complexity Of Binary Search
How much time binary search take on average to search for an element in the array ? Before we try to answer that question, let us understand the decision tree for binary search.
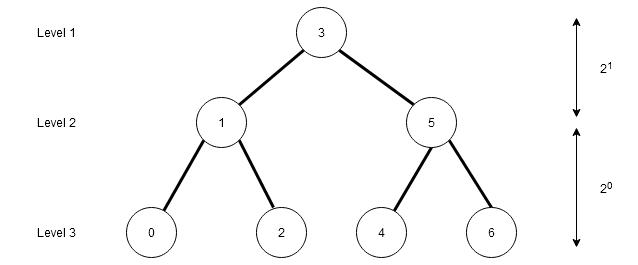
A decision tree is the pattern that the binary search follows to get to the element. Suppose that each of the node in binary search has two child including the root. Then the total number of nodes in the decision tree is given by the equation.
\begin{aligned}
&N <= 2^L - 1\\
&N + 1 <= 2^L\\
&Where \\
&N \hspace{1mm} is \hspace{1mm}total \hspace{1mm} number \hspace{1mm} of \hspace{1mm} nodes\hspace{1mm} in \hspace{1mm} the\hspace{1mm} decision\hspace{1mm} tree.\\
&L \hspace{1mm} is \hspace{1mm} the \hspace{1mm} number\hspace{1mm} of \hspace{1mm}levels\hspace{1mm} in \hspace{1mm} the\hspace{1mm} decision\hspace{1mm} tree.
\end{aligned}The decision tree above is from an array of size where
is the mid value. If we compute other mid values we get the above decision tree. The difference between parent and child is
where
.
Relationship between Nodes and Elements of Sorted Array
In the above decision tree, we have number of elements that match with the tree. Each of the node in the decision tree has exactly 2 child. But this is not possible all the time because number of elements of an array for binary search can be different.
Therefore,
\begin{aligned}
&N + 1 >= n + 1\\
&where \\
&N + 1 \hspace{1mm}is \hspace{1mm}the\hspace{1mm} number\hspace{1mm} of\hspace{1mm} nodes\hspace{1mm} in the\hspace{1mm} tree\\
&n + 1\hspace{1mm} is \hspace{1mm}the \hspace{1mm}number \hspace{1mm}of \hspace{1mm}elements\hspace{1mm} in \hspace{1mm}the \hspace{1mm}array
\end{aligned}Using the above information we can say that
2^L >= N + 1 >= n + 1
Taking log of equation will give us, . Therefore, the time complexity of binary search in average and worst case is given as
.
C++ Implementation of Binary Search
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
int main()
{
int S[10] = { 6, 23, 34, 42, 48, 54, 65, 75, 81, 95};
int key,low,high;
int mid= 0;
//Read key value
cout <<"Enter your key:" ;
cin >> key;
low = 0;
high = 9;
//Binary search
while(low <= high)
{
mid = low + (high - low)/2;
if (key < S[mid])
{
high = mid - 1;
}
else if ( key > S[mid])
{
low = mid + 1;
}
else
{
cout <<"Key found at " << mid << ": " << S[mid]<<endl;
return mid;
}
}
}Input:
Enter your key: 65Output:
Key found at 6: 65In the next article, we will discuss another variant of binary search called the interpolation search.
