Transpose Sequential Search

Table of Contents

Earlier you learned about linear search which search for a key from a given array. The search is affected by whether the array is ordered or unordered. The performance get better if the key is found at the beginning of the array. The transpose sequential search does that for repeated searches. It is also known as self-organizing linear search.

With each time you search for a key in the array, the transpose sequential search will shift the key at the beginning of the array. Therefore, next time you search for the same key you will find it in less time.

Transpose Sequential Search Algorithm

//Algorithm : Transpose Sequential Search
Algorithm Transpose_Sequential_Search(S, n, K)
{
     i := 0
     while (i < n and K != S[i]) do 
     {
          i := i + 1         // move through the array as long as K is not matching any element
     }
     if K = S[i] then
     {
          print ("Key found !")
          swap( S[i], S[i-1])
     }
     else
     {
          print ("Key not found !")
     }
}

In the algorithms above,

$K$ – It is the search key which we are trying to locate in the array.

$S [0: n-1]$ – It is the array of numbers.

$n$ – it is the number of elements in the array.

Example #1

Suppose there is an array $S$ of $10$ numbers and we want to search for a key $K$ . We will do the usual search, but repeat our search several times for the same key $K$ . This will show us the use of transpose sequential search in repeated searches.

Let \hspace{1mm}S[0: 9] = \{ 42, 54, 10, 59, 32, 11, 77, 21, 99, 66 \} \hspace{1mm} and \hspace{1mm} search \hspace{1mm} key \hspace{1mm} be \hspace{1mm} K = 99.

We will do repeated search for $K$ in following way.

99, 10, 99, 32, 99

In between our searches, we are trying to search other numbers also, so that it look natural. With each search attempt the original array will change in following way.

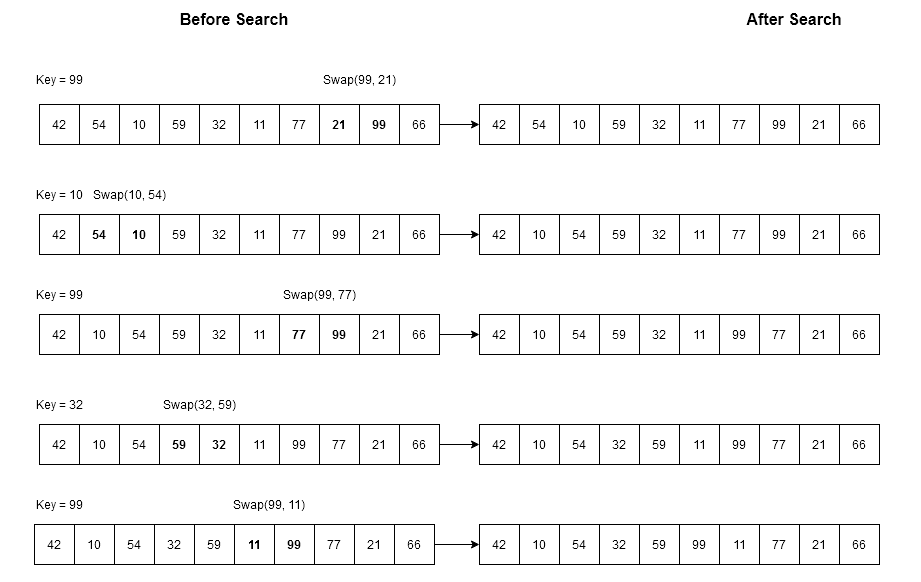
Figure 1 - Each search attempt will improve the position of search key 99 — Figure 1 – Each search attempt will improve the position of search key 99

Each of the search will swap the search key with its previous element, if we are searching for $99$ , first it gets found and then it is swapped with previous element $21$ initially. With each subsequent search the position of $99$ goes to the beginning of the array.

Time Complexity of Transpose Sequential Search

If the search key $K$ is at the end of the array then it is worst case scenario and time taken is $O(n)$ . Each search attempt improves the position and the search is done in constant time $O(1)$ .

C++ Implementation of Transpose Sequential Search

PROGRAM : TRANSPOSE SEQUENTIAL SEARCH
#include <iostream.h>
#include <stdio.h>
int main()
{
//Declare all variables and the array
 int S[] = { 42, 54, 10, 59, 32, 11, 77, 21, 99, 66 };
 int K;
 int temp = 0;
 int n = 10;
 int i = 0;
 // Read the input value
 cout << "Input the value of K: ";
 cin >> K;
 while (i < n && K != S[i])
 {
    i = i + 1;           //Move through the array
 }
 if(K == S[i])
 {
    cout << "Key Found!" << endl;
    //swap
    temp = S[i];
    S[i] = S[i-1];
    S[i-1] = temp;
    cout << S[i-1];
 }
 else
 {
    cout << "Item not found" << endl;
 }

 return 0;
}

Input:

Input the value of K: 99

Output :

Key Found!
99

In the next article, you will learn about some other forms of linear search algorithms.