Interpolation Search Algorithm

Table of Contents

The interpolation is an advanced version of binary search algorithm. It performs better than the binary search algorithm for large data sets.

Interpolation Search

Algorithm interpolation_search(S, n, Key)
{
    low := 0
    high := n - 1
    mid := 0

    while ((S[high] != S[low]) && (key >= S[low]) && (key <= S[high])) {
        mid = low + ((key - S[low]) * (high - low) / (S[high] - S[low]));

        if (S[mid] < key)
            low = mid + 1;
        else if (key < S[mid])
            high = mid - 1;
        else
            return mid;
    }

    if (key = S[low])
        return low 
    else
        return -1
}

In the above pseudo code we have following

S[ ] – It is the array with n elements.

n – It is the number of elements in the given array.

Key – it is the search key we are trying to locate within the array.

low – lowest index which start at 0

high – highest index which is n-1 if low starts at 0.

mid – middle value of the array.

How Interpolation Search Works?

Suppose you have to search a number between 0 to 99. You are given an array of size 10 to search and all number are equally distributed. Consider the image below.

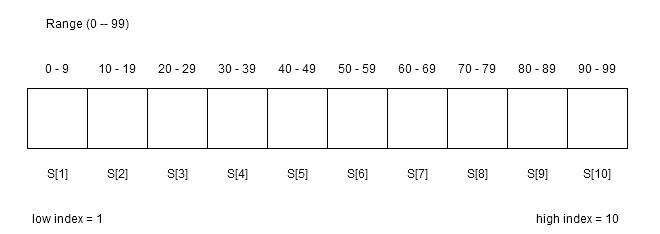
Figure1- DistribFigure1- Distribution of numbers into 10 array positions with low = 1 and high =10

Each position has a separate range of number possible because the array must be sorted. So, in first position we can have any number from 0-9 and second position we can have a number between 20-29 and so on.

The numbers may or may not be equally distributed. Suppose if the numbers are equally distributed as per the figure below.

Advertisements

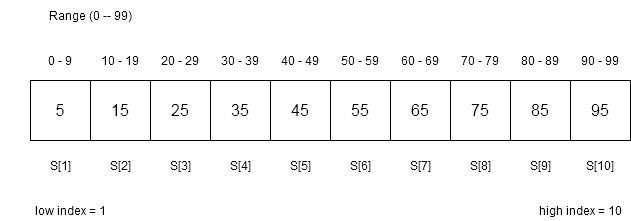
Figure2 -Sorted array with equally distributed values.

The interpolation search will use the following equation to probe the position of middle (mid) element. If right index is found return the index or continue the probe.

mid = low + (x - S[low]) * (high - low)/(S[high] - S[low])

Suppose we want to search for x = 35 from the array. Then using the above equation, we get,

mid = 1 + ( 35 - 5 ) * ( 10 - 1 ) / ( 95 - 5 ) 
= 1 + 30 * 9 / 90
= 1 + 270/ 90
= 1 + 3 => 3
Therefore, S[4] = 35

We were directly able to probe the correct position of the search key 35.

Let us consider another situation where array is not distributed equally, however, the array is sorted in non-decreasing order. See the image below.

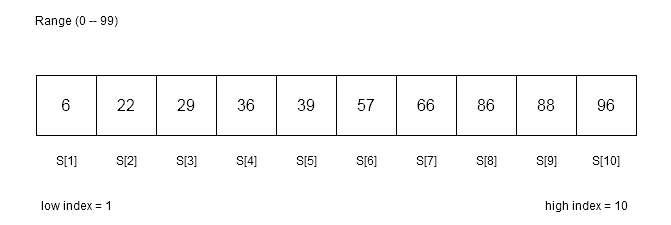
Figure 3 - Interpolation array is not distributed equally,but sorted in non-decreasing order — Figure 3 – Interpolation array is not distributed equally,but sorted in non-decreasing order

In this array, we must search for key = 86 using interpolation search technique. The algorithm determine if the search key falls within the range S[low] and S[high], otherwise it will report false and terminate.

The next step is to compute the mid value using equation of mid.

mid = 1 + (86 - 6 ) * ( 10 - 1 ) / ( 96 - 6 )
mid = 1 + ( 80 * 9 ) / 90
mid = 1 + 720/90
mid = 1 + 8 = 9
S[9] = 88

We did not get the right value in the first iteration; therefore, interpolation search will run another iteration to find the search key = 86.

If key < S[mid] then 
high = mid - 1

Then run the interpolation search again.

low = 1
high = 9 - 1 = 8
S[1] = 6
S[8] = 86
x = 86 
mid = 1 + ( 86 - 6 ) * (8 - 1)/ (86 - 6)
mid = 1 + 80 * 7 / 80
mid = 1 + 7 
mid = 8
S[8] = 86 
Key is found !

Binary Search and Interpolation Search

By probing the correct position or even closer to the key in an array, the interpolation search takes full advantage of the sorted array where binary search will take more steps by splitting the array into half the size repeatedly. In smaller searches the binary search may be faster than interpolation search, but if you have an extremely big data to search interpolation search algorithm will take less time.

In the above example, to search for key = 86, the interpolation search took 2 steps to complete. The above computation will give you an idea that the binary search is not good when compared with interpolation search while working on a large data set.

Time Complexity

On average the interpolation search perform better than binary search.The time complexity of binary search in average case and worst case scenario is $O( log \hspace{1ex} n)$ .

The interpolation search on average case has $O(log (log \hspace{1ex} n))$ assuming that the array is evenly distributed. If the array is increasing exponentially then the worst case happens. Then we must compare the search key to each element of the array. This will give a time complexity of $O(n)$ .

C++ Implementation of Interpolation Search

#include <iostream.h>
#include <stdio.h>
#include <conio.h>
int main()
{
   int S[10] = { 6, 22, 29, 34, 43, 57,66, 86, 88, 96};
   int key,low,high;
   int mid= 0;
   //Read key value
   cout <<"Enter your key:" ;
   cin >> key;
   low = 0;
   high = 9;
   //Interpolation search
   while((S[low] != S[high]) && (key >= S[low]) && ( key <= S[high]))
   {

      mid = low + ((key - S[low]) * (high - low)/(S[high] - S[low]));

      if (S[mid] < key)
      {
	low = mid + 1;
      }
      else if ( key < S[mid])
      {
	  high = mid - 1;
      }
      else
      {

      cout <<"Key found at " << mid << ": " << S[mid]<<endl;
      return mid;
      }
   }

   if ( key == S[low])
   {
      return low;
   }
   else
   {
      return -1;

   }

   }

Input

Enter your key:22

Output

Key found at 1: 22