Linear Search Algorithms

The linear search is the simplest search where we try to find an element K from the list L. We have to compare K with each and every item in the list. The search is affected when the list if sorted or unsorted.

Linear Search

Suppose we want to find search key from array with elements

\{ s_1, s_2, s_3, s_4,\cdots,s_n \}

There is two possible situations.

• The array is ordered from lowest to highest.
• The array is unordered.

If the array is sorted then the search is called an ordered linear search. If a search is performed on unordered array then it is called an unordered linear search.

Unordered Linear Search

Algorithm Ordered_Linear_Search ( S, n, K)
{
// S[0: n-1] is the array with n sorted elements
// n is the total number of elements in the array
// K is the key we are trying to find in the array S

i : = 0
while (i < n and K > S[i]) do   //keep moving through the elements
{
      i := i + 1
}
if K = S[i] then
      print("Key found!")
      return(i) // return the index of the element found
else
      print("Key not found!")
}

In the above algorithm, we have following:

– An array with n elements that is sorted already.

– It is the number of elements in the array. The array starts with index and that last element has an index of .

– It is the value we are searching within the array. If found then algorithm return the location index of else it will simply print “Not found”. is called the search key.

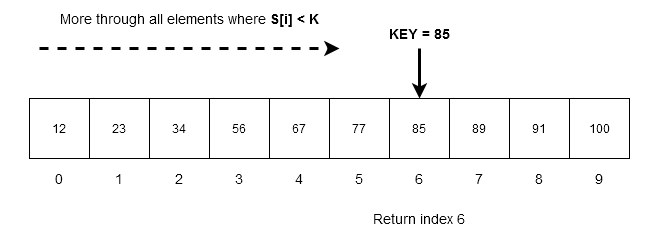
Example #1

Suppose we have an array of numbers,

S[0: 9] = \{ 12, 23, 34, 56, 67, 77, 85, 89, 91, 100 \}

We want to search for in the array. The algorithm goes through each item in the array as long as

• is greater than element , that is, is greater than any element in the array keep moving.
• When is equal to any element ,that is, . We have found the element successfully and return the index value.

In the above example, are less than ; therefore, search algorithm will skip all of these elements and stop at which is true. The index is returned.

Note that the ordered linear search will not continue anymore and terminate successfully.

Time Complexity of Ordered Linear Search

Since the array is ordered, it is easy to compute the time complexity. If the search key is at the beginning which is the best case, it takes constant time to find the element.

What if the element is not available ? The algorithm goes through each and every element in the array. If array has n element then the complexity is which is the worst case.

C++ Implementation Of Ordered Linear Search

//PROGRAM: ORDERED LINEAR SEARCH
#include <iostream.h>
#include <stdio.h>
int main()
{
//Declare all variables and the array
 int S[] = {12,23,34,56,67,77,85,89,91,100};
 int K;
 int n = 10;
 int i = 0;
 // Read the input value
 cout << "Input the value of K: ";
 cin >> K;
 while (i < n && K > S[i])
 {
    i = i + 1;           //Move through the array
 }
 if(K == S[i])           //Check if the key is equal to any element in the array
 {
    cout << "Key Found!" << endl;
    cout << "Location = " << i << endl;
 }
 else
 {
    cout << "Item not found" << endl;
 }

 return 0;
}

Program Input :

Input the value of K: 85

Program Output:

Key Found!
Location = 6

Unordered Linear Search

The unordered linear search is where the array has unordered elements. If we want to search for the key, then we must go through all elements.

Algorithm Unordered_Linear_Search ( S, n, K)
{
// S[0: n-1] is the array with n sorted elements
// n is the total number of elements in the array
// K is the key we are trying to find in the array S

i : = 0
while (i < n and K != S[i]) do   //keep moving through the elements until a match is found
{
      i := i + 1
}
if K = S[i] then
      print("Key found!")
      return(i) // return the index of the element found
else
      print("Key not found!")
}

The above algorithms is similar to ordered linear search, however it does not search in ascending order or descending order. The array may contain the key value at any location.

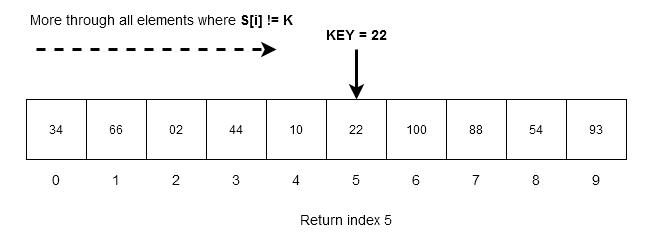
Example #2

Suppose an unordered array contain following elements,

S[0: 9] = \{ 34, 66, 02, 44, 10,100, 22, 88, 54, 93 \}

We want to search for in the array. The algorithm goes through each item in the array as long as elements are not equal to the key.

Time Complexity of Unordered Linear Search

The time complexity is very much similar to ordered linear search. If you locate the element at the beginning of the search then the complexity is and worst case it is .

But, think about search on average the ordered array will stop searching as soon as the right element is found and unordered array has to go through all elements because the key could be scattered anywhere.Therefore, ordered linear search perform better on average.

C++ Implementation Of Unordered Linear Search

#include <iostream.h>
#include <stdio.h>
int main()
{
//Declare all variables and the array
 int S[] = {34, 66, 2, 44, 10, 22, 100, 88, 54, 93 };
 int K;
 int n = 10;
 int i = 0;
 // Read the input value
 cout << "Input the value of K: ";
 cin >> K;
 while (i < n && K != S[i])
 {
    i = i + 1;           //Move through the array
 
 if(K == S[i])
 {
    cout << "Key Found!" << endl;
    cout << "Location = " << i << endl;
 }
 else
 {
    cout << "Item not found" << endl;
 }

 return 0;
}

Program Input:

Input the value of K: 22

Program Output:

Key Found!
Location = 5

In the next article, you will learn about other linear search algorithms.