The hash table is perfect solution to store dictionary where each data is uniquely identified using a key. The dictionaries are implemented using arrays. The key are stored with the object itself and each data element has its own index value. Therefore, data is stored in the array as key-value pair.
The hash table uses a hash function which is a mathematical function to compute a hash value which is the index L of the data element in the array. The hash function uses key
to compute
.
The hash table allows three types of operations.
- Insertion of a new value.
- Deletion of an existing value.
- Search for a value in the array.
Direct Addressing Scheme
The hash table uses a numerical key or characters that are converted to numeric equivalent for computing the hash value where
is the index of data element in the array.
Suppose is the universal set of all keys from where we use
to map
from an array of size
It means every
is mapped to every
. Also, no two keys have same hash value.
This type assigning a unique value to each an every data element in array is called direct-addressing.
Example
In this example, our universe U = { all English letters } from where we get our keys . The size of the array is
where
is equal to
, the size of the array.
Each letter is a key is converted to a number equivalent to its position in the English alphabets. For example, A = 1, B = 2, and so on.
| Key | Hash Function | Hash Value |
| A | H(A) | 1 |
| B | H(B) | 2 |
| C | H(C) | 3 |
| D | H(D) | 4 |
| T | H(T) | 20 |
| V | H(V) | 22 |
| X | H(X) | 24 |
| Y | H(Y) | 25 |
| Z | H(Z) | 26 |
The direct-addressing is fine as long as the size of the data elements are small in number. Therefore, using a unique key for each an every element is impractical and difficult to maintain. We can use a small subset of keys from universal set of keys
where
.
Another problem with direct addressing is computer memory, we cannot store all the values of array because memory size is limited.
Finally, the direct addressing requires you to use the whole array regardless of whether you want to store anything or not. The empty spaces are wasted.
Hash Function
If we are to use a small subset of keys such that maps all elements of array
where
is the size of the array. Each array position has an index value
.
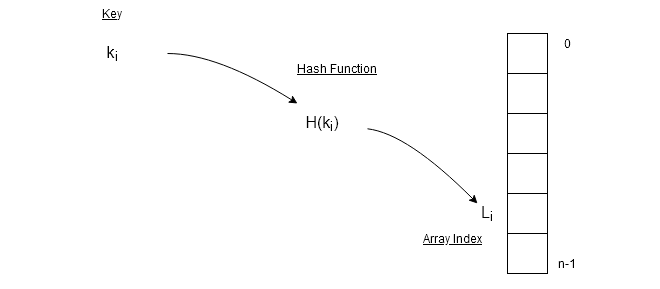
Hash function is a mathematical function such as a mod function which is a popular method of computing hash value. If range of the array is , for any key
,
\begin{aligned}
&H(k_{i}) = L_{i}\\
&H(k_{i}) = k_{i} \hspace{2 mm} MOD \hspace{2 mm} N
\end{aligned}The MOD function takes a value as key and gives remainder as output. In this way, more than one key value or index will have same hash value.
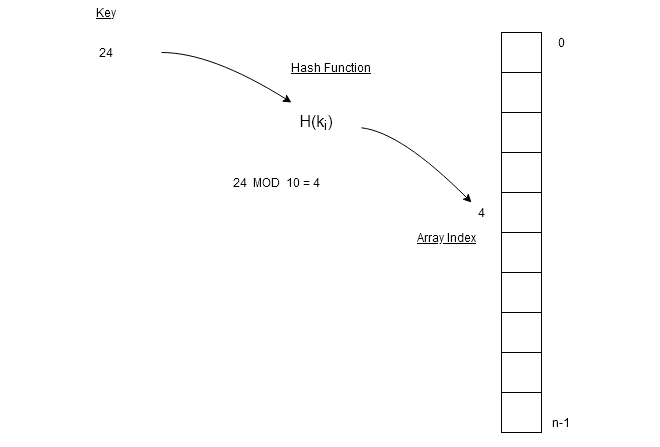
In the figure above, we have key and
which is size of the array. A MOD operation on key
gives
which is the location of the data element in the array.
Similarly, if , then hash value is
again. Therefore, we want a hash function which always gives same results for a key. The key values with same hash value are called synonyms.
Synonyms
We can treat hash value or index in an array as a bucket holding slots for each synonym. So, a bucket can be can have
slots. Such type of representation requires a two-dimensional array where a row indicates buckets with slots.
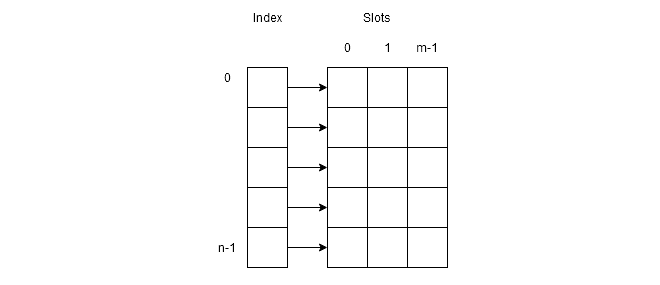
The figure above shows that the first column of the two dimensional array is buckets and other columns are slots.
Example
Let be set of keys and size of array be
. The hash function we are going to use is
.
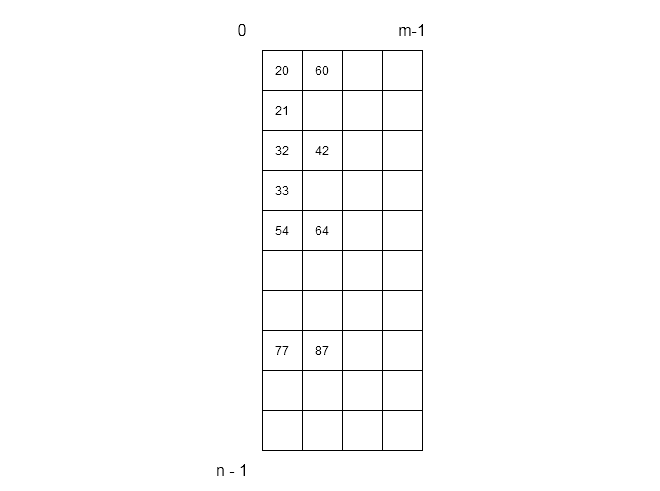
Each of the row in above figure has 3 slots per bucket to store values that have same hash values. for example,
\begin{aligned}
&77\hspace{2 mm} MOD \hspace{2 mm}10 = 7\\
&87\hspace{2 mm} MOD \hspace{2 mm} 10 = 7
\end{aligned}Since, two slot have same value, it will cause problem during hash table operations – insertion, deletion and search.
Collision
When hash value is computed using hash function and if two keys and
has same hash value then it cause a collision.
\begin{aligned}
&H(k_{i}) = H(k_{j})
\end{aligned}Therefore, there are two important method of solving the problem of managing synonyms.
- Linear open addressing
- Chaining
In the future posts, we will talk about each of these methods in detail.
