In the previous article, you learnt about set notations – the roster notation and the set builder notation. In this article, I will discuss about the types of sets available. This is part 1 where we see basic types of sets and in part 2, I will discuss some derived types.
Set Types
The sets are collections of objects with some properties, but not all sets are same. Mathematicians have identified that certain sets have special properties and named them accordingly.
We have different type of sets, listed here.
- equal set
- equivalent set
- empty set
- singleton set
let us understand each of these set type. Also, I am giving examples of each set type so that it is easy to understand. For more examples, you can refer to some math books.
Equal Sets
We can define the equal set informally as
” Two sets are equal if and only if they have the same elements.”
If ![]() and
and ![]() are two equal sets, elements are set
are two equal sets, elements are set ![]() are in
are in ![]() and elements of set
and elements of set ![]() is in set
is in set ![]() . It means
. It means ![]() and
and ![]() are equal sets, if and only if
are equal sets, if and only if
\begin{aligned} \forall x ( x \in A \iff x \in B) \end{aligned}![]() (For all) is a universal quantifier, which is considering all elements from a set or universe. The symbol (
(For all) is a universal quantifier, which is considering all elements from a set or universe. The symbol (![]() ) is biconditional, meaning
) is biconditional, meaning ![]() is only true if
is only true if ![]() is also in
is also in ![]() or
or ![]() is only true when
is only true when ![]() is in
is in ![]() .
.
To represent an equal set, we write
A = B
For example, Let ![]() be set
be set ![]() .
.
A = \{3, 6, 2\}and ![]() be set
be set ![]() .
.
B = \{6, 2, 3\}Both ![]() and
and ![]() are equal (
are equal ( ![]() ), since, they have the same elements. Here order of elements does not matter.
), since, they have the same elements. Here order of elements does not matter.
Equivalent sets
The equivalent set is defined as:
“Two or more set are equivalent if their cardinality is same”.
Here cardinality is simply meaning number of elements and shown as a function of set.
Therefore,
If ![]() and
and ![]() are two sets then they are equivalent if and only if
are two sets then they are equivalent if and only if
n(A) = n(B)
For example, let ![]() and
and ![]() are
are ![]() sets.
sets.
\begin{aligned}
&A = \{ 3, 1, 7\}\\
&B = \{p, q , r\}\\
&C = {4, 3, 2, 8, 9}\\
&D = {1, x, 3, y, 8}
\end{aligned}The elements of set ![]() are
are ![]() which are numbers. and elements of set
which are numbers. and elements of set ![]() are
are ![]() and
and ![]() which is alphabets. The elements of set
which is alphabets. The elements of set ![]() are numbers and elements of set
are numbers and elements of set ![]() are both numbers and alphabets.
are both numbers and alphabets.
First, we determine the cardinality of sets – ![]() and
and ![]() using the cardinality function.
using the cardinality function.
\begin{aligned}
&n(A) = 3 \\
&n(B) = 3 \\
&n(C) = 5 \\
&n(D) = 5 \\
\end{aligned}The cardinality of set ![]() and set
and set ![]() is
is ![]() , so they are equivalent sets. The cardinality of set
, so they are equivalent sets. The cardinality of set ![]() and Set
and Set ![]() is
is ![]() , so they are another equivalent set.
, so they are another equivalent set.
Note that the elements don’t have to be same. Set with different types of elements can be equivalent.
Comparison between equal and Equivalent set
Let us compare between equal sets and equivalent sets.
- Two or sets have same elements, so they can be equal and equivalent at the same time.
- For equivalent sets, the elements does not matter, only cardinality is important, whereas equal sets consider elements also.
- order of elements in both equal and equivalent sets does not matter.
- empty sets are always equivalent to each other.
When two sets have same element, they are equal set which we know already, but they have the same cardinality also. For instance,
\begin{aligned}
&A = \{2, 5 , 7\}\\
&B = \{5, 2, 7\}
\end{aligned}The set ![]() and
and ![]() are same, hence, equal sets. If we check the cardinality of both sets, then
are same, hence, equal sets. If we check the cardinality of both sets, then
n(A) = 3\\n(B) = 3
It means that the number of elements is also same for both functions.
Another thing to notice in set ![]() and set
and set ![]() is that order of elements is different. The order of elements is does not matter in equal sets. Also, it does matter how the elements are arranged when we are only concerned with number of elements of the set. Therefore, equivalent sets are also not affected by the order of elements in a set.
is that order of elements is different. The order of elements is does not matter in equal sets. Also, it does matter how the elements are arranged when we are only concerned with number of elements of the set. Therefore, equivalent sets are also not affected by the order of elements in a set.
Empty sets
The empty sets are sets with no elements. They are denoted with ![]() or
or ![]() . Sometimes a set is described in terms of properties. For example,
. Sometimes a set is described in terms of properties. For example,
Set of months in a year.
If the set property is such that there is no element exists is also empty.
For example,
A set of numbers with ![]() , it is not possible, so such a set contains no element, and it is an empty set. It is also called the null set.
, it is not possible, so such a set contains no element, and it is an empty set. It is also called the null set.
The empty set is this symbol ![]() and this
and this ![]() is a set that contains empty set.
is a set that contains empty set.
Singleton Set
A singleton set is a set with only one element.
For example,
Set of even prime, ![]() is only one element
is only one element ![]() .
.
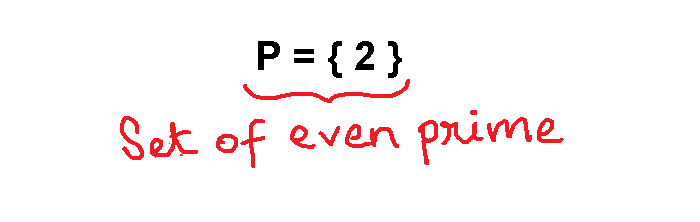
Other examples of singleton sets are :
\begin{aligned}
&Set \hspace{3px} A = \{ 0 \}\\
&or \\
&Set \hspace{3px} B = \{ x \in \mathbb{Z} \mid x + 4 = 0 \}
\end{aligned}
Where ![]() can be only one number which is
can be only one number which is ![]() in set
in set ![]() .
.
Finite Sets
All of the previous set types have one thing in common, which is, the number of elements is limited or countable. A set with limited element is called a finite set. There is no special symbol to denote a finite set.
But, when you use roster notation, then you can list all the elements of the set. In other words, roster method is most suitable way to show a finite set.
For example, the set of all number less than ![]() perfectly divisible by number
perfectly divisible by number ![]() are:
are:
\begin{aligned}
S = \{ 5, 10, 15, 20, 25 \}
\end{aligned}Note, how set builder notion is very descriptive and long while describing a set of finite elements. That’s why a roster method is best choice for represent finite sets.
What happens when the set has infinite number of elements ?
Infinite Sets
A set with infinite number of elements is known as infinite set. It this set elements are many, to roster method is not a suitable method to represent the set.
Consider an example,
N = \{Set \hspace{3px} of \hspace {3px} natural \hspace{ 3px} numbers \}The natural numbers are infinite and uncountable set. If that is the case, then describing the natural number set using set builder notation is suitable option.
It does not mean that infinite sets cannot be showed as using roster notation. But you must use the ![]() symbol to show that there are infinite number of elements in the set.
symbol to show that there are infinite number of elements in the set.
Therefore, the set of natural numbers can be represented as:
N = \{ 1, 2, 3, 4, \cdots \}The set of integers grows continuously on both direction, which is negative and positive. Therefore, it is shown as:
Z = \{ \cdots, -3, -2, -1 , 0, 1, 2, 3 , \cdots \}There are several examples of infinite sets in mathematics. You will learn those in future articles.
Summary
You learnt that the sets are broadly finite or infinite sets. Depending on element in the sets. So a two sets can be equal or equivalent depending on number and type of elements in them. There are empty or singleton sets with no or one element respectively.
