Before we start with this lesson. Here are some questions to test yourself about this new topic.
Q1. Identify the variables and constants in following expression.
\begin{aligned}
&2x + 5\\
&5y - 3x + 6
\end{aligned}Q2. What is quotient of 25 and 5?
Q3. Identify whether following is an expression or an equation.
\begin{aligned}
&24 + 5\\
&45x = 4 + 2x\\
&5x - 3y
\end{aligned}Try to answer them on your own, and I will tell you the answers at the end of the article.
Understanding Expressions
In this article, you will know how to translate word problems to expressions. But before that you must know what an expression is. To explain the expression, you must know the building blocks of an expression. The different parts are given below.
You will learn about
- Variables,
- Constants,
- Operators,
- Expressions
- Translate word problems into expressions.
Let’s start with a small example.
Variables and Constants
Every year the price of orange changes and the price of apples becomes Rs 10 more than the price of Oranges.
If orange price for a year is Rs 24 per orange, then apple price is Rs 34 per apple which is Rs 10 more than oranges.
Next year the price becomes Rs 43 , then apple price increase to Rs 53.
In algebra, we call orange price as variable, and the Rs 10 that we add to get the price of apples is called a constant.
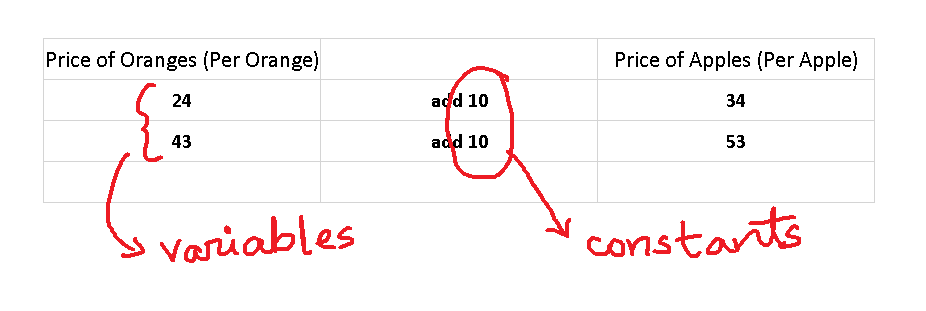
Let say price of orange is x then the price of apple would be x + 10.
\begin{aligned}
&Orange \hspace{4px}Price = x\\\\
&Apple \hspace{4px} Price = x + 10
\end{aligned}A variable value does not remain the same, because it is changing frequently, but a contant value remain same, like the number 10.
Expression is made of variables, or constant or combination of variables, constants, and operators.
Operators
Operators are like instruction in algebra, to do something with the variables and constants. You can say that they connect variables and contants to do something called the math operations. After which you get a result.
We can do basic arithmetic operations like:
- Add
- Subtract
- Multiply
- Divide
For add use plus symbol, minus for subtraction, multiply is ‘cross’ symbol, that is sometimes confused with letter ‘x’ so we use a ‘dot’ symbol for multiplication now. Sometimes, two numbers separated by parantheses is also taken as multiplication.
Divide is a special symbol and some times we can use fraction to represent a division.
For Example,
a plus b is ‘a’ and plus symbol and ‘b’.
similarly,
‘c’ multiplied by ’12’ is ‘c’ and ‘multiplication symbol’ and ‘ number 12’.
35 divided by 5 is ‘number 35’ and divide symbol and ‘number 5’. You can create several examples like this.
There are operators for compare two quantities in algebra.
It is called the inequality operators which are:
- equal to
- not equal to
- less than
- greater than
- less than or equal to
- greater than or equal to
The inequality operators are used to compare two expressions or numbers to find out how much one number or expression is different from the other.They might be equal or not equal, or may be one is greater or less than the other.
You can use the appropriate operators in your expressions.
For example,
a is equal to b is ‘b’ and “equal to’ symbol and ‘b’.
These are the building blocks of an algebraic expressions.
Types of Expressions
The expressions are of two types.
- Numeric expressions
- Algebraic expressions.
Numeric Expressions
When you don’t use any variables, then expression is made of just numbers, it is called numeric expressions.
for example,
number 2,
3 – 5,
6 + 5 (4),are numeric expressions.
Algebraic Expressions
Similarly, when an expression has variables, as well as constants, it is called algebraic expressions.
For example,
y
x + b
3x – 4
are algebraic expressions.
The main difference between these two expressions are that numeric expression can be evaluated down to a single value.
algebraic expression cannot be evaluated to a single value unless we know the value of the variables in the expression.
Word Expressions
Sometimes expressions are given in the form of phrases, and you must find the arithmetic operation and the numbers from the phrases given.
Words that indicate addition is:
- the sum of 4 and 7
- 4 plus 7
- 7 more than 4
- 4 increased by 7
- the total of 4 and 7
- 7 added to 4
All of these phrases indicate adding a number to another number, and you can translate it into addition expression:
For example, 4 + 7
Similarly, phrases that indicate subtraction are:
- 3 minus 1
- the difference of 3 and 1
- 1 subtracted from 3
- 3 decreased by 1
- 1 less than 3
all of these phrases are equal to the expression 3 minus 1.
Similarly,
- 5 times 3
- the product of 5 and 3
indicate multiplication and can be written as:
5 * 3, 5(3), or (5)(3)
The phrases that indicate division are:
- 10 divided by 5
- the quotient of 10 and 5
- the ratio of 10 and 5
- 5 divided into 10
Converting Phrases to Expressions
So, you write these phrases into expression as
10 divide symbol and 5, other forms of expression are 10 forward slash 5, and the ration form 10 by 5.
Let translate some phrases to expression.
- six added to seven
- the quotient of 100 and x.
The first expression asks to add six to number 7, so the expression is:
7 + 6
The second phrases ask to divide 100 by x. This is an algebraic expression. It is
100 by x
Similarly, you can translate any expression into phrases that indicate an arithmetic operation.
To explore more on this topic, you read and practice from algebra books.
Solution to Quiz
The answers to the question I asked at the beginning of this video are:
Q1: Identify the variables and constants from expressions
- 2x + 5 and
- 5y – 3x + 6
Here the variables are letter, and all numbers are constants. So, in the first expression variable is x and constants are 2 and 5.
In the second expression, x and y are variables, constants are 5, 3, and 6.
Q2. What is the quotient of 25 and 5.
Given phrase, asking quotient meaning it is division of 25 by 5. So the answer is 25 divided by 5.
Question 3 ask to identify expressions and equations.
the first one is
24 + 5 which is a numeric expression.
The second one is
45x = 4 + 2x, which is equation because two expressions are compared using an equal sign.
The third one is:
5x – 3y, which is an algebraic expression.
Summary
In this lesson, you have learned the building blocks of expression and know how to convert a word expression to algebraic expression. Also, algebraic to word expressions.
