3-Variable K-Map

by

The K-map or Karnaugh map is a graphical tool to minimize a boolean function. From the previous article, you know how a boolean function represented in canonical sum of product is changed into sum of product form using K-map. Also, the k-map is nothing but the same truth table in a matrix form where each of the cell is a minterm.

In this post, you will learn about a 3-variable with an example.

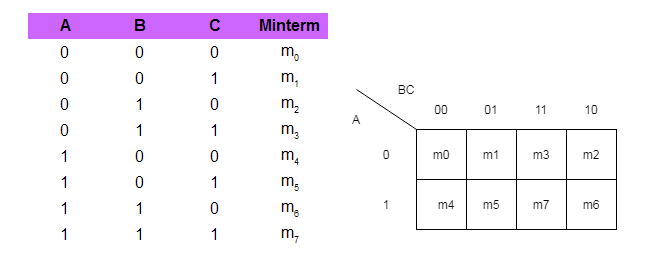
Truth Table for 3-Variable Map

It is a well-known fact that K-map is nothing but a different representation of truth table; therefore, a truth table for 3 variables will contain 2^3 = 8 rows. This also means that the K-map would contain total of 8 cells, each for a row in the truth table.

Consider the following truth table for three variables – A, B, and C.

Truth Table and 3 Variable K-Map
Figure 1 – Truth Table and 3 Variable K-Map

Let us understand the characteristics of the 3-variable K-map because it is very important to understand and use this map for boolean function minimization.

Characteristics of a 3-variable K-map

  • The truth table has total of 8 rows which corresponds to 8 cells of the 3-variable K-map.
  • Each cell differs in only one variable to its neighbor, both horizontally and vertically.
  • To minimize the terms in a boolean function, mark a cell as 1 if its output is 1 in the truth table and leave the rest as it is.
  • To minimize the variables within each term of a cell that has 1 in K-map, start making groups of 2, 4, and 8.
  • Grouping of 1s includes neighboring cells, corners and sides even though they overlap each other.
  • Make larger groups if possible.
  • Once all 1s are covered then you can stop.

Now that you know the 3-variable map and its characteristics. It is time to see an example.

3-Variable Map Examples

In this section, you will find examples of 3-variable map. These are some examples, you may refer to some textbooks for more examples and practice yourself.

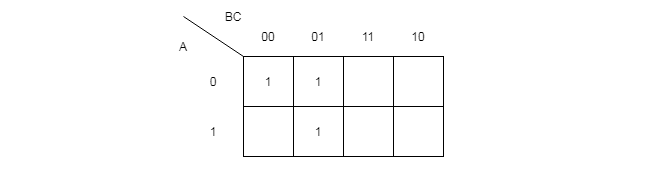
Q1 – Plot a 3-variable map for the following function.

F = A'B'C' + A'B'C + AB'C

Solution:

The function use three minterms that gives output 1 as per truth table.

Solution - Three variable map with cells marked which gives output 1
Figure 2 – Solution – Three variable map with cells marked which gives output 1

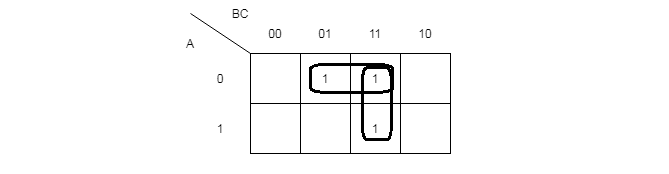
Q2 – Plot a three variable map and show grouping of two for marked cells for the following function.

F = A'B'C + A'BC + ABC

Solution:

Solution - Cells marked as 1s are grouped into groups of two
Figure 3 – Solution – Cells marked as 1s are grouped into groups of two

Q3 – Plot a three-variable map for following function and make group of four cells that are marked as 1s.

F = A'B'C' + A'BC' + AB'C' + ABC'

Solution:

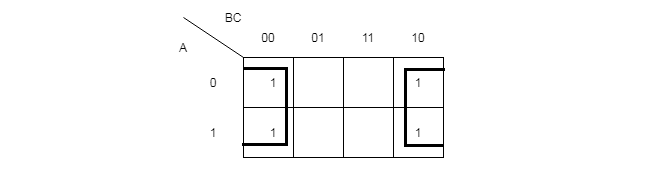
Solution - Sides are overlapped to make a group of 4 cells
Figure 4 – Solution – Sides are overlapped to make a group of 4 cells

You should note that both sides are overlapped and made into a group of 4 four because two side when compared have a difference of 1 variable, for example, A’B’C’ and A’BC’ has only difference of B’ and B. This applies to both – horizontal and vertical directions. The sides and corners are also neighbors of each other with a difference of 1 variable change.

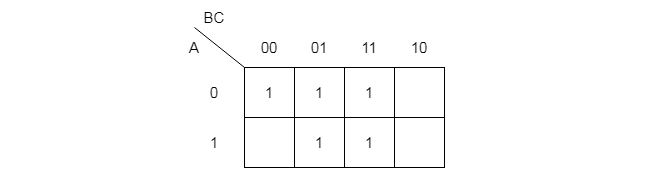
Q4 – Minimize the following Boolean function using K-Map.

F = A'B'C' + A'B'C + A'BC + AB'C + ABC'

Solution:

We will find the solution to this problem in step by step manner.

Step 1: Plot a 3-variable map and mark the terms from the function to 1.

Mark all the cells from the function as 1s.
Figure 5 – Mark all the cells from the function as 1s.

Step 2: Make groups of 2, 4, or 8 and only take variables that are common in the group both horizontally and vertically.

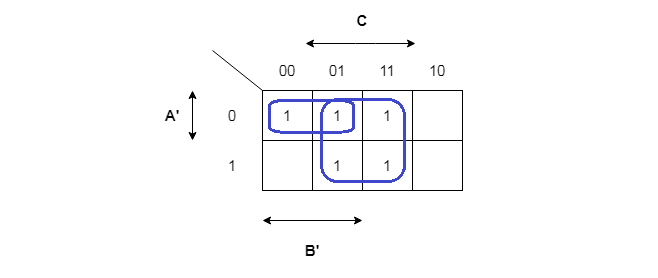
Make group of 2, 4 and 8 for cells with 1
Figure 6 – Make group of 2, 4 and 8 for cells with 1

Once you have grouped all the cells with 1s into group of 2s, 4s, or 8s. List all the variables that are common vertically and horizontally. For example

//Group of two
= A'B'C' + A'B'C 
= A' is common vertically
= B' is common horizontally
Our first term is A'B'.
//Group of four 
= A'B'C + A'BC + AB'C + ABC
= A' + A cancel out vertically, leaving B'C + BC
= C is only common variable horizontally.
Our second term is C.
The final minimized equation is F = A'B'+ C

Rules for grouping in 3-variable map

  • A single cell with 1 gives 3 literals.
  • Two adjacent cell group gives 2 literals.
  • Four cells with 1s will give a single literal.

In the next article, we will see how to minimize a Boolean function with 4-variable map which has 16 cells to work with.