Simplifying Boolean Function using K-Map -Special Case

by

K-Map technique is a straight forward and simple method for minimizing Boolean functions. In this article, you will learn a special case of K-map, when the function is in a Standard Sum of Product and not in a Canonical Sum of Product form.

Advertisements

For example

F = A'B'C' + ABC'            -  (1)

F = A'B + BC' + A'B          -  (2)

In function1, each term is called a minterm( A’B’C). The sum of minterms is called a Canonical Sum of Product. It can be directly taken from the Truth Table for the function.

The function2 has terms called a product term which may have one or more literal. The sum of all such terms is called a Standard Sum of Product. The same concept applies for Canonical Product of Sum form.

Now the problem is that if you are given a standard sum of product for Boolean minimization, what to do, because it appears that its already minimized.

Advertisements

How to simplify the function ( 2 )using K-Map?

Create a three variable map like we do always .and put 1 in the box where a particular term is missing .

A'B

Which term is missing? yes right!  it’s C

A'B( C + C')
A'BC + A'BC'

In the map you put 1 in the cell for both

A'BC + A'BC'

Similarly, Solve other missing variable in each of the terms of the function.

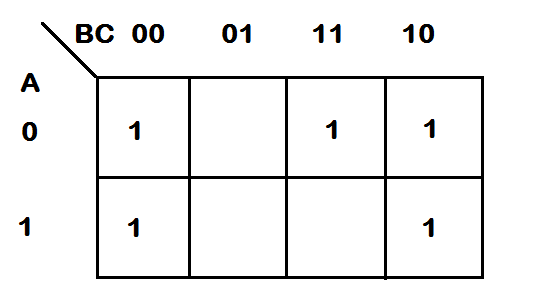
KMAP for F = A'B + BC' + A'B
Figure 1 – K-MAP for F = A’B + BC’ + A’B

Now, you can minimize the above 3-variable K-Map easily because you have identified the correct boxes.

Advertisements