7 total views
Numbers are everywhere and used in many places – financial institution, statistics, engineering and so on. Without number system our daily life would be difficult.
Humans use a number system called the decimal number system and everyone can easily understand this system. You go to a store to buy something, you need a number system to count your money. Even a small thing such as making a list of its need numbers.
Contents
What is a number system?
A number belonging to a number system with:
- A base
- Coefficient
that is between 
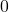to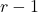 
.
Examples
Decimal with r=10 and coefficient a = 0 to 9 Binary with r=2 and coefficient a = 0 and 1 Octal with r= 8 and coefficient a = 0 to 7 Hexadecimal with r=16 and coefficient a = 0 to 9, A, B, C, D, E, F
Converting from any number system to decimal system
If the base and coefficients are given, then any number can be converted to decimal system using following
\begin{aligned}
a_{n}\cdot r^{n}+\cdots+ a_{1}\cdot r + a_{0}+a_{-1}\cdot r^{-1}+a_{-2}\cdot r^{-2}+ a_{-n-1}\cdot r^{-n-1}+ \cdots + r^{n}
\end{aligned}Example
To convert binary number
into decimal number, do following
\begin{aligned}
&1011 = 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 2^0\\\\
&= 8 + 0 + 2 + 1\\ \\
&= 11
\end{aligned}11 is decimal equivalent of .
Example
Convert 
into decimal equivalent.
Solution:
\begin{aligned}
&Integer \hspace{5px} part \rightarrow 1101\\\\
&1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0\\\\
&8 + 4 + 0 + 1\\\\
&13\\\\
&Decimal \hspace{5px} part \rightarrow .011\\\\
&0 * 2^-1 + 1 * 2^-2 + 1 * 2^-3\\\\
&0 + \frac{1}{4} + \frac{1}{8}\\\\
&\frac{3}{8}\\\\
&Answer = 13 + \frac{3}{8} = \frac{(13 * 8 + 3)}{8}\\ \\
&= \frac{107}{8}\\ \\
&= 13.37
\end{aligned}Conversions from Decimal to Other Number Systems
The decimal number system have a base 
and coefficients ranging from 
.
Decimal to Binary
To convert from decimal from binary, divide the decimal number repeatedly until no longer possible to divide. Each time you get a quotient and remainder, divide the quotient and note the remainder. The remainders of this division put together in reverse order is the answer. See the example below.
For the fractional part, you need to multiply the decimal fraction with base repeatedly until you reach or close to zero for the fractional part. When you multiply a fraction with base , you get two thing – an integer and a fraction.
If the fraction has not reached zero or real close to zero, multiply it with base in next iteration and check the integer and fraction part. The integer part put together is the binary equivalent for the decimal fraction. See the example below
Problem:
Convert 
to binary equivalent number.
Solution:
\begin{aligned}
&\frac{25}{2} \hspace{1cm}quotient = 12, remainder = 1\\\\
&\frac{12}{2}\hspace{1cm} quotient = 6, remainder = 0\\\\
&\frac{6}{2} \hspace{1cm}quotient = 3, remainder = 0\\\\
&\frac{3}{2}\hspace{1cm} quotient = 1, remainder = 1\\\\
&\frac{1}{2}\hspace{1cm} quotient = 0, remainder = 1\\\\
\end{aligned}Now we find the fractional part binary equivalent.
\begin{aligned}
&0.13 \cdot 2 = 0.26 => 0 + .26\\\\
&0.26 \cdot 2 = 0.52 => 0 + .52\\\\
&0.52 \cdot 2 = 1.04 => 1 + .04\\\\
&Answer: - 11001 + .001 = 11001.001
\end{aligned}Note that the integer part is remainders written in reverse order, that is, bottom to top in the first part of the solution.
Decimal to Octal
The decimal to octal conversion is done in the same way as decimal to binary except the base 
. For example
Problem:
Convert 
to its octal equivalent.
Solution:
\begin{aligned}
&\frac{235}{8}\hspace{1cm} quotient = 29, remainder = 3\\\\
&\frac{29}{8} \hspace{1cm}quotient = 3, remainder = 5\\\\
&\frac{3}{8} \hspace{1cm}quotient = 0, remainder = 3\\\\
&Answer: - 353
\end{aligned}Decimal to Hexadecimal
The hexadecimal number has a base 
and we need to divide decimal number with base to get the hexadecimal equivalent, but hexadecimal digits 
are 
.
\begin{aligned}
&\frac{2344}{16} \hspace{1cm}quotient = 146, remainder = 8\\\\
&\frac{146}{16} \hspace{1cm}quotient = 9, remainder = 2\\\\
&\frac{9}{16} \hspace{1cm}quotient = 0, remainder = 9\\\\
&Answer: The \hspace{5px} hexadecimal \hspace{5px}equivalent \hspace{5px}of \hspace{5px}2344\hspace{5px} is \hspace{5px}928.
\end{aligned}Conversions to Binary
Octal to Binary
To convert octal to binary, convert each digit of the octal number to its binary equivalent, but you are only allowed to use 3-bit positions because of 
which is the maximum range of octal coefficient. For example
Problem:
Convert 
into its binary equivalent.
Solution:
\begin{aligned}
&2 \rightarrow 0 1 0\\\\
&5 \rightarrow 1 0 1\\\\
&6 \rightarrow 1 1 0\\\\
&Answer: The \hspace{5px}binary \hspace{5px}equivalent \hspace{5px}is \hspace{5px}010 \hspace{5px}101 \hspace{5px}110
\end{aligned}Hexadecimal to Binary
We use 4 bits to convert each digit in a hexadecimal number to get the binary equivalent. This is because 
in decimal, the maximal value allowed in hexadecimal number. For example
Problem:
Convert 
into binary equivalent.
Solution:
\begin{aligned}
&2\hspace{1cm} C \hspace{1cm} D\hspace{1cm}3\\
&0010\hspace{12px}1100\hspace{17px}1101\hspace{17px}0011\\\\
&The\hspace{5px} binary\hspace{5px} equivalent \hspace{5px} of \hspace{5px} 2CD3 \hspace{5px} is \hspace{5px} 0010 \hspace{5px} 1100\hspace{5px} 1101 \hspace{5px} 0011
\end{aligned}Binary to Other Number Systems
Binary to Octal
To convert from binary to octal use 3-bit position and convert it into its decimal equivalent.
- For integer part 3 bit from left to right
- For fractional part 3 bit from right to left
This will give you the octal equivalent of binary number. For example,
\begin{aligned}
&1001.0101 \rightarrow 001 \hspace{5px}110\hspace{5px} . 010 \hspace{5px}100\\
&\hspace{2cm}1 \hspace{15px} 6 \hspace{15px} . 2 \hspace{15px} 1\\\\
&Answer: - The\hspace{5px} octal\hspace{5px} equivalent \hspace{5px}is \hspace{5px}16.21.
\end{aligned}Binary to Hexadecimal
Group the given binary number into a group of four and then convert the each of the group into the decimal equivalent to get the hexadecimal digit and group all the digits found to get the hexadecimal number. For example
Problem:
Convert the given binary number 110101011100 into hexadecimal equivalent.
Solution:
Given binary number can be separated into group of four.
\begin{aligned}
&110101011100 \rightarrow 1101 \hspace{5px}0101 \hspace{5px} 1100\\
& \hspace{2.65cm}13\hspace{15px} 5 \hspace{19px}12\\
&\hspace{2.65cm}D \hspace{16px} 5 \hspace{20px} C
\end{aligned}Therefore, the hexadecimal equivalent number is D5C.
Other Number Systems
Octal to hexadecimal
We use a very simple procedure to convert octal to hexadecimal number. You can do this two easy steps.
- Convert Octal to Binary number.
- Convert the Binary number obtained into hexadecimal.
In the previous section, we learned about converting octal to binary and binary into hexadecimal. In this section, you have to use that knowledge in converting octal to hexadecimal. For example,
Problem:
Convert the given octal number 
into Hexadecimal equivalent.
Solution:
Step 1: Convert the octal into binary number.
\begin{aligned}
&2 \hspace{1cm} 3 \hspace{1cm}4\\
&010\hspace{17px} 011 \hspace{17px} 100
\end{aligned}Step 2: Convert the binary number into a hexadecimal number.
\begin{aligned}
&Binary \hspace{5px}Number \rightarrow 010011100\\
\end{aligned}Step 3: Group the binary number into groups of four bits from left to right.
\begin{aligned}
& 0000 \hspace{5px}1001 \hspace{5px}1100\\
&0 \hspace{2em}9 \hspace{2em}12
\end{aligned}Step 4: Convert the result into a hexadecimal number.
Therefore, the hexadecimal equivalent is 
.
Hexadecimal to Octal
If you reverse the process given in octal to hexadecimal conversion, you will get an octal equivalent for hexadecimal number.
References
- John.F.Wakerly. 2008. Digital Design: Principles And Practices, 4/E. Pearson Education, India.
- Mano, M. Morris. 1984. Digital Design. Pearson.
- NATARAJAN, ANANDA. 2015. Digital Design. PHI Learning Pvt. Ltd.
Bestseller
Digital Design: With an Introduction to the Verilog HDL, VHDL, and System Verilog 6th Edition
A modern update to a classic, authoritative text, Digital Design, 5th Edition teaches the fundamental concepts of digital design in a clear, accessible manner. The text presents the basic tools for the design of digital circuits and provides procedures suitable for a variety of digital applications. Like the previous editions, this edition of Digital Design supports a multimodal approach to learning, with a focus on digital design, regardless of language. Recognizing that three public-domain languages―Verilog, VHDL, and System Verilog―all play a role in design flows for today’s digital devices, the 5th Edition offers parallel tracks of presentation of multiple languages, but allows concentration on a single, chosen language.