In the previous lesson, we learned about binary codes and how they are used for representing a distinct discrete element of information using 1s and 0s.
People use the decimal system for everything and it’s easier for them to use decimal numbers on a computer than binary numbers. But binary is what the computer understands.
So we need a system to convert decimal to binary and perform the calculation using binary numbers and convert the output back to decimal for users. This binary representation of a decimal number is called the binary coded decimal code or BCD code.
Binary-Coded Decimal (BCD code)
The binary coded decimal is a 4-bit code and each 4-bit code represents one decimal digit from 0 to 9. See the table below
| Decimal Digit | Binary Coded Decimal |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
But there are 16 codes because ![]() combinations. The codes from
combinations. The codes from ![]() to
to ![]() does not matter and are not used in BCD.
does not matter and are not used in BCD.
For example
The binary and BCD value of 128 is given below for your understanding.
| Binary number for 12810 | BCD Code for 12810 |
| 1000 0000 | 0001 0010 1000 |
Important points to remember
- Decimal number is
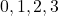 so on, and BCD code is
so on, and BCD code is 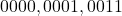 … It means they are same.
… It means they are same. - The binary number is not BCD, there is a difference.
- BCD coded decimal numbers need more bits. See the example above.
BCD Addition
When two BCD numbers are added then two things happen
- Sum is less than
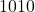 = decimal
= decimal 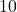
- The sum is equal to or more than decimal
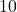
Suppose you add following BCD numbers
\begin{aligned}
&4 + 3\\
&0100\\
&0011\\
&-------\\
&0111 = 7_{10}
\end{aligned}The result is a BCD sum and less than ![]() .
.
First Case – when BCD sum does not have a carry
Consider another example
\begin{aligned}
&4 + 3\\
&0100\\
&0011\\
&-------\\
&0111 = 7_{10}
\end{aligned}\begin{aligned}
&8 + 4\\
&1000\\
&0100\\
&-------\\
&1100 = 12_{10}
\end{aligned}The BCD does not allow 1100 and we need 12 as an answer in BCD. The first digit is 1 and the second digit is 2.There are 16 codes in BCD and we are using only 10 of them.
1010 + 0110 = 1 \hspace{3px} carry + 0000 = 0001 0000 = 10 \hspace{3px} in \hspace{3px}BCD \\
1011 + 0110 = 1 \hspace{3px}carry + 0001 = 0001 0001 = 11 \hspace{3px} in \hspace{3px} BCD\\
1100 + 0110 = 1\hspace{3px} carry + 0010 = 0001 0010 = 12 \hspace{3px} in \hspace{3px}BCD\\
1101 + 0110 = 1 \hspace{3px}carry + 0011 = 0001 0011 = 13 \hspace{3px} in \hspace{3px}BCD\\
1110 + 0110 = 1 \hspace{3px}carry + 0100 = 0001 0100 = 14 \hspace{3px} in \hspace{3px}BCD\\
1111 + 0110 = 1 \hspace{3px}carry + 1000 = 0001 0101 = 15 \hspace{3px} in \hspace{3px}BCDThen whenever, you get an invalid BCD sum, add a 0110 = 6 to the result and you will get the correct BCD sum.
Second Case – when BCD sum has a carry
We now look at another case of BCD sum when the result appears to be correct, but it has a carry.
\begin{aligned}
&\hspace{13px}8+9\\
&\hspace{13px}1 0 0 0\\
&+1 0 0 1\\
&-----------\\
&\hspace{8px}1 0 0 0 1
\end{aligned}In this case, we still add ![]() to the 4 least significant bits.
to the 4 least significant bits.
\begin{aligned}
&1 0 0 0 1\\
&\hspace{5px}0 1 1 0\\
& ------\\
&1 0 1 1 1\\
& = 1 \hspace{4px} carry + 0111\\
& = 0001 0111 = 17
\end{aligned}Example – BCD Addition
In this example, we will add two decimal numbers,
\begin{aligned}
&\hspace{12px}14 \hspace{10px}+ \hspace{10px}389 = 603\\
&\hspace{12px}0 0 1 0 0 0 0 1 0 1 0 0 = 214\\
&+0 0 1 1 1 0 0 0 1 0 0 1 = 389\\
&-----------\\
&\hspace{10px}0 1 1 0 1 0 1 0 1 1 0 1\\
&\hspace{2.9em}0 1 1 0 0 1 1 0\\
&------------\\
&\hspace{10px}0 1 1 0 0 0 0 0 00 1 1 = 603
\end{aligned}References
- John.F.Wakerly. 2008. Digital Design: Principles And Practices, 4/E. Pearson Education, India.
- Mano, M. Morris. 1984. Digital Design. Pearson.
