A Boolean function is expressed in two form.
- Sum of Minterms
- Product of Maxterms
Sum of Minterms
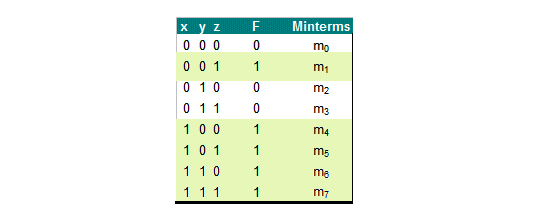
x’ y’ z , x y’ z’ , x y’ z , x y z’ , x y z , gives 1 as output in the above Truth Table.
- Literal – x, y, A, b etc is a label which denote an input variable for a logic gate. Literal can be normal or complimented.
- Minterm – product of two or more literal using ANDing of each literal.
- Maxterm – sum of two or more literal using ORing of each literal.
Before we understand what sum of minterm or product of maxterm is, we must understand a few terminology.
For example,
x or x', y or y'For example,
x.y.z or x'ySuppose we have 2 variable – x and y, then all possible combination of literals are x’y’ , x’y, xy’, xy. If we have 3 variables then all combination of literals are as follows.
Basically, if there are n variable, then there is 2^n. For 3 variable, there are 2^3 = 8.
A minterm is the term from table given below that gives 1 output.Let us sum all these terms,
F = x' y' z + x y' z' + x y' z + x y z' + x y z
= m1 + m4 + m5 + m6 + m7
F(x,y,z) = ∑(1,4,5,6,7) is known as Sum of Minterms Canonical Form.Why is it called canonical form ? because all the literals present in each of the terms.
Product of Maxterm
The Product of Maxterm is complement of the Sum of Minterm of a function. To obtain the Product of Maxterm, we need two step process.
- Find those minterms in the Truth Table that gives a 0 as output.
- Complement those minterms using DeMorgan’s law.
Let us now apply the above to obtain the Product of Maxterm form.
From the previous truth table given, x’ y’ z’, x’ y z’, x’ y z gives output as 0.
F = x' y' z' + x' y z' + x' y z by Rule 1
= (x' y' z' + x' y z' + x' y z)' by DeMorgan's Law
= (x + y + z)(x + y' + z)(x + y' + z') Product of Maxterms formWe see that the Product of Maxterm is ANDing of all ORed terms.
