4-Variable K-Map - Notesformsc

Table of Contents

Previous post, you learned about 3-variable K-map, and learned how to minimize a boolean function. In this post, you will learn about bigger map such as a 4-variable K-map. With 4-variable map you will be able to make larger groups of cells.

Plotting a 4-variable K-map

The 4 variables of a Boolean function will give a truth table of about $4^2 = 16$ rows of input combinations. These can be directly translated to 16 cell 4-variable K-map. See the following figure.

Figure 1 – Truth Table and 4-Variable K-Map

Grouping of cells in a 4-variable K-map

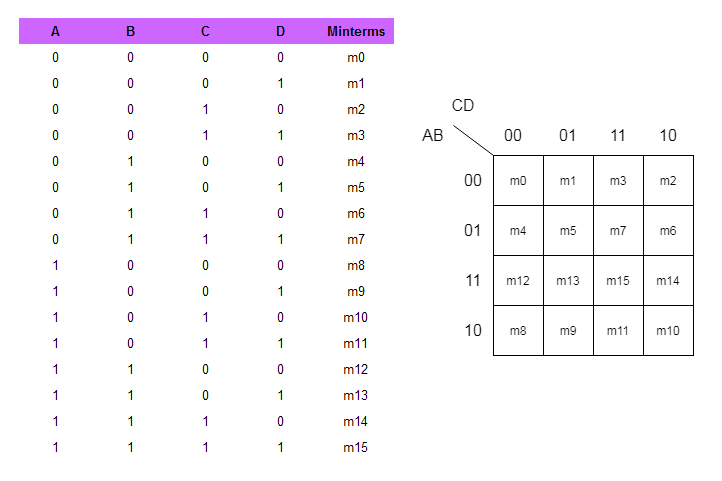
While you minimize a boolean function using 4-variable K-map, group the cell with 1s into 2s, 4s, and 8s, and so on. See the figure below.

Figure 2 - Grouping Of 2, 4 and 8 respectively — Figure 2 – Grouping Of 2, 4 and 8 respectively

Rules for Grouping of cells

Here are some simple rules when group cells.

Single cells with 1 gives you a term with 4 literals.
Two adjacent cells will minimize and give you a term with 3 literals.
A grouping of 4 cells of 1s will give you a term with 2 literals.
A grouping of 8 cells of 1s will give a single literal.

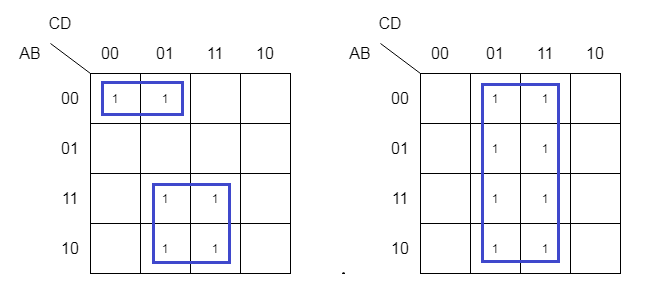
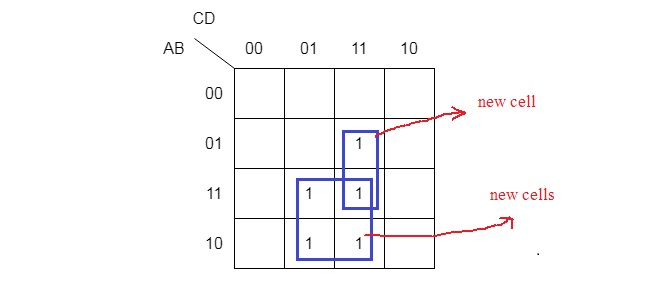
Therefore, you must always try for maximum number of 1s in a group. Some group overlap each other as we mentioned in earlier in previous post. Each overlapping group must include one uncovered cell that contains a 1. See the figure below to understand this.

Figure 3 - Overlapping groups — Figure 3 – Overlapping groups

4-Variable K-Map Example

In this section, I have given few examples of 4-variable K-maps. For more practice, you can refer to some textbooks with lot of exercises.

Q1: Minimize the following Boolean function using 4-variable K-map.

F(A,B,C,D) = ∑(0,1,2,4,5,6,8,9,12,13)

Solution:

Step 1: Construct a 4-variable K-map and mark all minterms with 1.

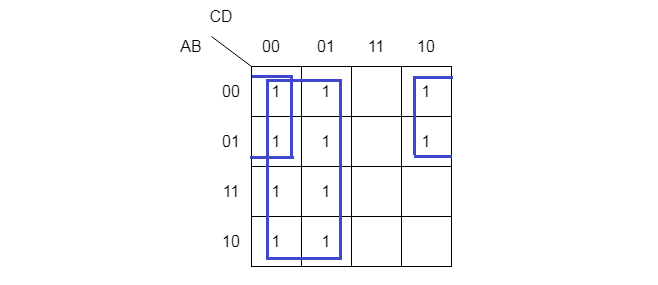
Step 2: Look vertically in a selected group and extract any common variable. Also look horizontally, extract any common variable from the group.

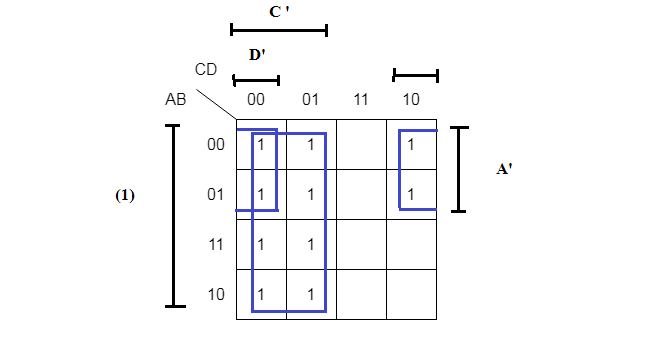
Figure 2 – Extract all common variables horizontally and vertically

In the group of four, horizontally, you get D’ and vertically, you get A’. Together it is a term of two literal, that is, A’D’. Similarly, the group of 8, vertically everything cancels out and leave just 1 because A’B’ + A’B = A’ and AB + AB’ = A, finally, A’ + A = (1). But, horizontally, for the group of 8, you get C’. Always the group of 8 will give you single literal.

Step 3: Write down all the solution.

Group of 8 = C'
Group of 4 = A'D'
The final expression is F = A'D' + C'

Verify the Solution using Algebraic Method

Let’s verify our solution using Boolean algebraic method.

F(A,B,C,D) = ∑(0,1,2,4,5,6,8,9,12,13)
F = A'B'C'D' + A'B'C'D + A'B'CD' + A'BC'D'+ A'BC'D + A'BCD' + AB'C'D' + AB'C'D + ABC'D' + ABC'D
F = A'B'C'(D' + D) + A'CD'(B' + B) + A'BC'(D' + D) + AB'C'(D'+ D) + ABC'(D' + D)
F = A'B'C' + A'CD' + A'BC' + AB'C' + ABC' 
F = A'C'(B' + B) + AC'(B' + B) + A'CD'
F = A'C' + AC' + A'CD'
F = C'(A' + A) + A'CD'
F = C' + A'D' // variable C has no effect hence removed

From the solution above it is clear that the 4-variable K-map is a simple solution to minimize a Boolean function with 4 variables.