In this post, you will learn example problems from combinational circuits. These problems help in minimizing Boolean functions and constructing logic circuit diagrams. The solution to the problems are given in step-by-step manner with explanation wherever possible.
Q1. Simplify the Boolean function using K-MAP technique.
F(A,B,C,D) = Σ( 0,1,4,8,9,10)There are 4 variables in this function. First, we construct a Truth Table for four variable functions. We can see that there are 16 minterm ![]() of which following gives a output value of 1.
of which following gives a output value of 1.
Solution:
Σ( 0,1,4,8,9,)
= m0 + m1 + m4 + m8 + m9 + m10
= A'B'C'D' + A'B'C'D + A'BC'D' + AB'C'D' + AB'C'D + AB'CD' 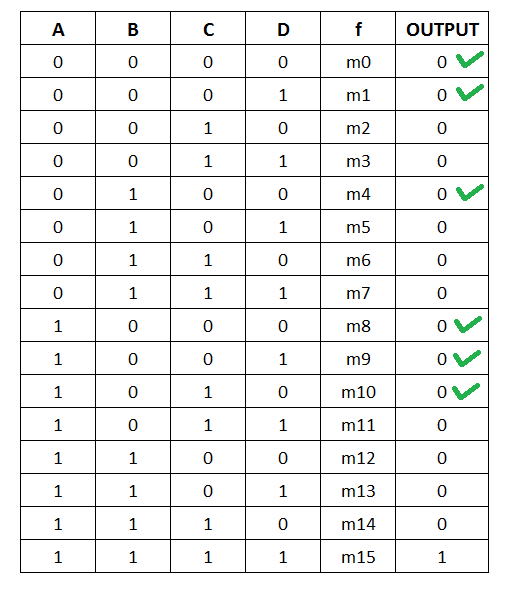
But you want the minimized Boolean function.
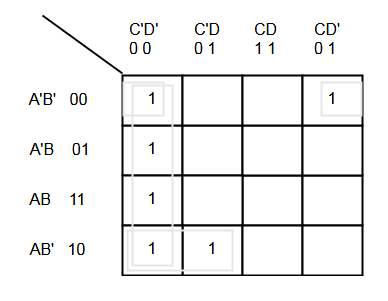
K-Map is great technique to reduce the minimize the Boolean function. Those minterms that give 1 is marked in the 4-variable K-map. Next, we need to group the adjacent 1s into group of 2, 4 and 8.Once grouped you can minimize the function using following method.
- Eliminate any common variable that negate each other – row wise or column wise (e.g.,
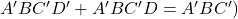 because
because 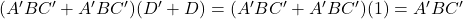
- After elimination a group of two adjacent 1s will give 3 variables term(e.g.,
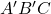 ).
). - After elimination a group of four adjacent 1s will give 2 variable term (e.g.,
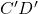 ).
). - Aftter elimination a group of eight adjacent 1ss will give 1 variable (e.g,
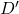 ).
).
Group 1 = A'B'C'D' + A'B'CD' = A'B'D'
Group 2 = A'B'C'D' + AB'C'D' + ABC'D' + A'BC'D'
= B'C'D' + BC'D'
= C'D'
Group 3 = AB'C'D' + AB'C'D' = AB'C'we have found 3 minimized minterms of our function.
= A'B'C' + A'D' + C'DB'Q2. Construct Logic Diagram of the following function using XOR and AND gates only,
F = A.B'CD' + AB'CD' + A.B'C'D + A'BC'D Solution:
F = (C.D')(A.B' + B'A) + (C'D)(A.B' + B.A')
F = (C.D')(A ⊕ B) + (C'D)(A ⊕ B)
F = (C.D' + C'D) (A ⊕ B)
F = (C ⊕ D) (A ⊕ B)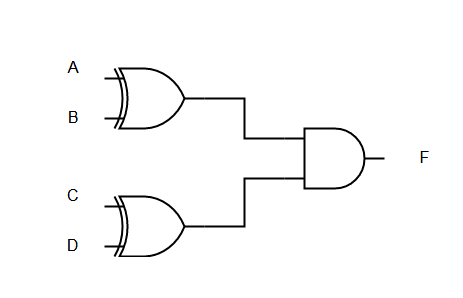
Q3. Draw the logic diagram corresponding to the following Boolean expression without simplifying them.
F=BC' + AB + ACD
F = (A + B) (C + D')(A' + B + D)Solution: (a)
F=BC' + AB + ACD 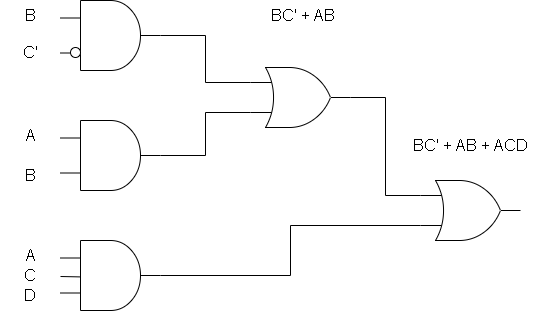
Solution: (b)
F = (A + B) (C + D')(A' + B + D)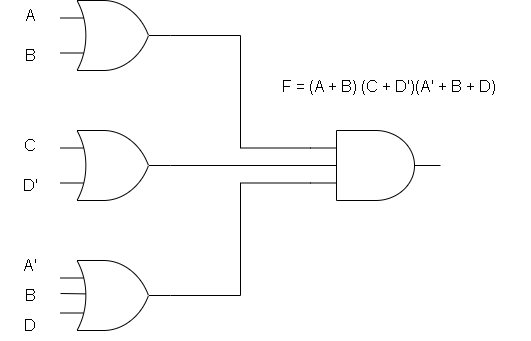
Q4. Express in Sum of Minterm and Product of Maxterm
F(x,y,z) = (x.y + z)(x.z + y)Solution:
F (x,y, z) = (x.y + z) (x.z + y)
=(x + z)(y + z)(x + y)(z + y)
=(x + z)+(y . y') . (y + z ) + ( x . x') . ( x + y )+ (z . z').(z + y)+( x . x' )
=( x + y + z).(x + y' + z).(y + z + x).(y + z + x').(x + y + z).(x + y + z').(z + y + x).(z + y + x')
= (x + y + z) . (x + y' + z) . (x' + y + z) . (x . y . z')
= M0 . M2 . M4 . M1
Π( 0,1,2,4) [ Product of maxterm form]
F = ∑(3 , 5, 6, 7) [ Sum of Product form]Q5. Express the complement of the function in terms of minterms.
a) F(A,B,C,D) = ∑(0,2,6,11,13,14).
b) F(x,y,z) = Π(0,3,6,7)Solution:
a) F(A,B,C,D) = ∑(0,2,6,11,13,14)
= m0 + m2 + m6 + m11 + m13 + m14
Complement of F is F' and it contains those minterms not there in F. Also this is a 4 variable function to there are 24 = 16 minterm
So, F' = m1 + m3 + m4 + m5 + m7 + m8 + m9 + m12 + m15
F' = ∑(1,3,4,5,7,8,9,12,15)