Concurrency conditions

There are certain conditions for concurrency. Here we have listed them for you in this article.

Conditions for Concurrency

$R(S_i) = \{ a_1, a_2, a_3, \cdots , a_m \}$ , the read set for $S_i$ , is the set of all variables whose values are referenced in statement $S_i$ during its execution.

$W(S_i) = \{b_1, b_2, b_3, \cdots, b_n \}$ , the write set for $S_i$ , is the set of all variables whose values are changed or written by the execution of statement $S_i$ .

Example #1

Consider the statement.

$C:= A - B$

The read set:

$R(C:= A - B) = \{A, B\}$

The write set:

$W(C:= A - B) = \{C\}$

The intersection of $R(S_i)$ and $W(S_i)$ need not be null.

Example #2

Consider following statement:

$X:= X + 2$

The read set:

$R(X:= X + 2) = \{ X \}$

The write set:

$W(X:= X + 2) = \{ X \}$

Bernstein’s Conditions

The following three conditions must be satisfied for two successive statements $S_i$ and $S_j$ to be executed concurrently and still produce the same results known as Bernstein’s conditions.

$R(S_1) \cap W(S_2)= \{ \}$ .
$W(S_1) \cap R(S_2) = \{ \}$ .
$W(S_1) \cap W(S_2) = \{ \}$ .

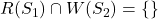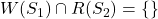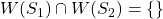Example:

Consider the following statements.

$S_1: a:=x-y$ .
$S_2: b:=z-1$ .

$R(S_1) = \{ x, y \}$ .
$R(S_2) = \{ z \}$ .
$W(S_1) = \{ a \}$ .
$W(S_2) = \{ b \}$ .

In the example above, all three conditions are satisfied. Therefore, the statement $S_1$ and $S_2$ can be executed concurrently.

We could use the precedence graph, but the precedence graph cannot be used in programming as it is a two-dimensional object. Moreover, it only shows the dependency relationship between statements.