In this article, you will learn about deadlock prevention method – Banker’s algorithm and Resource allocation graph. You will also learn about 4 conditions for deadlock.
Let’s start with the resource allocation graph.
Resource Allocation Graph
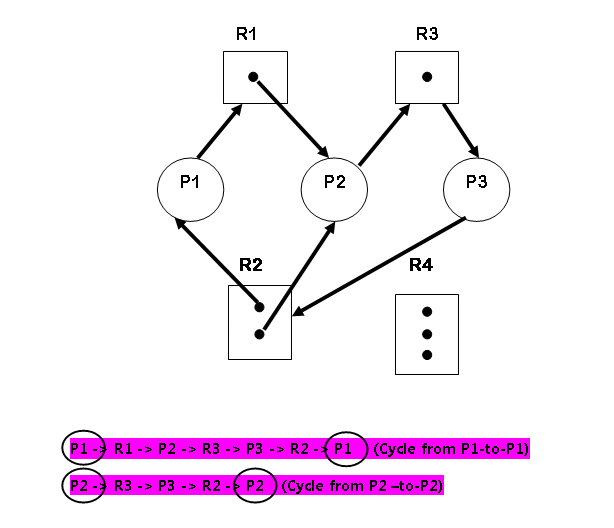
Resource Allocation graph describes the deadlock more precisely. It has a set of vertices V and set of edges E.
Vertices types
Vertices are divided into
![]() set of active processes in the system.
set of active processes in the system.
![]() set of vertices that represent the resources.
set of vertices that represent the resources.
Edge types
![]() means
means ![]() has requested resource
has requested resource ![]() and waiting for it is called request edge
and waiting for it is called request edge
![]() means that the instance of resource
means that the instance of resource ![]() is allocated to process
is allocated to process ![]() called the assignment edge.
called the assignment edge.
Resource ![]() may have more than one instance.
may have more than one instance.
Example:
Vertices
\begin{aligned}
&P = {P_1, P_2, P_3}\\\\
&R = {R_1, R_2, R_3, R_4}
\end{aligned}Instances of Resource
\begin{aligned}
&R_1 = 1\\
&R_2 = 2\\
&R_3 = 1\\
&R_4 = 0
\end{aligned}Edges
\begin{aligned}
&Request \hspace{3px}Edges: \hspace{3px}P_1 \rightarrow R_1, P_2 \rightarrow R_3\\\\
&Assignment \hspace{3px}Edges: R_1 \rightarrow P_2, R_3 \rightarrow P_3, R_2 \rightarrow P_1, R_2 \rightarrow P_2\\\\
&R_2 \rightarrow P_1 \rightarrow R_1 \rightarrow P_2 \rightarrow R_3 \rightarrow P_3 \hspace{3px}(No \hspace{3px} Cycle)\\\\
&R_2 \rightarrow P_2 \rightarrow R_3 \rightarrow P_3 (No \hspace{3px}Cycle)
\end{aligned}*A CYCLE IN THE GRAPH IS BOTH A NECESSARY but not a SUFFICIENT CONDITION FOR A DEADLOCK.
* CYCLE INVOLVE A SET OF RESOURCES WHERE EACH RESOURCE HAS ONLY ONE INSTANCE.
THEN DEADLOCK OCCURS.
Methods for handling deadlock
- First method is to prevent deadlock
- the Second method is to deadlock avoidance by managing system resources. This is done by giving additional information about process request and whether that request can be satisfied.
- Another way is to let deadlock occur and place an algorithm that recovers the system from deadlock.
- If no algorithm is available for recovery, then the system must be restarted manually.
Deadlock Prevention
There are 4 conditions that must hold for a deadlock to occur and if we prevent any one of them from occurring when there is no deadlock.
Mutual exclusion
A non-sharable resource must give mutual-exclusive right to access it for any process. A sharable resource such a read-only file has no problem sharing the resource and does not need mutual-exclusive rights.
Mutual exclusive rights do not have an effect on deadlock prevention.
Hold and Wait
There are two ways this can be done.
- First allocate all the resource to the system before it executes.
- Second way, the process can be allocated resource only when it has none and if it requires an additional resource, leave the existing one.
Example:
Suppose a process copies files from DVD and then sorts them and print the result.
DVD player/writer, disk drive and printer must be allocated at the beginning itself using the first approach.
In the second approach, the first DVD drive the given and when the process finished with the DVD drive and reads all the information, it releases the DVD drive.
Next to Disk drive is allocated before copying the files to the disk drive and when a task is over it is released. Similarly, the printer does the printing for process and process release the printer.
No Preemption
If a process fails to get all the resource it needs, then it must release the resource it is already holding.
It will only start when all the resources including the new one are available.
If a process is available, allocate them otherwise check if it is held by some waiting process, if yes then preempt the waiting process and allocate to the requesting process.
This technique cannot be applied to I/O devices.
Circular Wait
Allocate resource in increasing order of enumeration. ![]() . Each process gets a number. We can say that there is a one-to-one function from resource to natural number.
. Each process gets a number. We can say that there is a one-to-one function from resource to natural number.
F: R -> N, where \hspace{3px}N \hspace{3px}is \hspace{3px}a \hspace{3px}set \hspace{3px}of \hspace{3px}natural \hspace{3px}numbers.Suppose there are three resources
\begin{aligned}
&F (tape \hspace{3px}drive) = 1\\
&F (disk \hspace{3px}drive) = 4\\
&F (printer) = 10
\end{aligned}First Process can request for any number of instances of the resource ![]() and after that, the process can request an instance of resource
and after that, the process can request an instance of resource ![]() if and only if
if and only if ![]() .
.
Deadlock Avoidance
Deadlock avoidance depends on additional information about how a request should be requested. The system can then make decisions based on currently available resource, the resource allocated to each process and future request & release of each process.
Each process must give prior information on the maximum resource of each type it needs. The system then uses deadlock-avoidance algorithms and checks the resource allocation state to check that a circular wait never occurs.
Safe State
A state is safe if the system can allocate resource to each process and still (to its maximum) in some order and still avoid deadlock. There exists a safe sequence.
Suppose there is a sequence of processes ![]() is a safe sequence for current allocation state if for each process,
is a safe sequence for current allocation state if for each process, ![]() request for a resource can be satisfied by currently available resources plus resources held by
request for a resource can be satisfied by currently available resources plus resources held by ![]() , where
, where ![]() .
.
If the resource for ![]() is not available, then it must wait till all
is not available, then it must wait till all ![]() have finished. Once a resource is obtained
have finished. Once a resource is obtained ![]() can execute and terminate and release all the resources.
can execute and terminate and release all the resources.
Then ![]() process competes for the resources and so on. If such a safe state does not exist, then the system is said to be in an unsafe state.
process competes for the resources and so on. If such a safe state does not exist, then the system is said to be in an unsafe state.
An unsafe state does not mean a deadlock state but it may lead to a deadlock state.
Deadlock-avoidance algorithm makes sure that resource is allocated to process only when it leaves the system in a safe state. Otherwise, it has to wait.
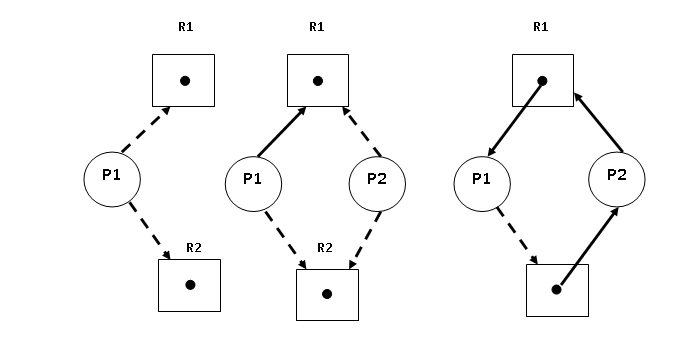
Resource-Allocation-Graph Algorithm
A new edge is introduced in the resource allocation graph called the Claim edge. ![]() means that it is a claim edge and shown as a dashed line in the resource allocation graph.
means that it is a claim edge and shown as a dashed line in the resource allocation graph.
A claim edge shows “Future requests” or “Future Assignments” and converted to request edge and assignment edge respectively.
The request is granted only if converting request edge to an assignment edge does not lead to the formation of a cycle in the graph, if the allocation to ![]() will form a cycle that will lead the system to an unsafe state, then the process
will form a cycle that will lead the system to an unsafe state, then the process ![]() must wait till the resource is available.
must wait till the resource is available.
Example:
\begin{aligned}
&P = \{P1, P2\}\\
&R = \{R_1, R_2\}
\end{aligned}| CLAIM EDGE | CONVERT TO REQUEST EDGE | CONVERT TO ASSIGNMENT EDGE |
| YES | YES | |
| YES | YES | |
| NO (Make a cycle) | NO | |
| YES | NO (P1 using R1) |
Banker’s Algorithm
The algorithm works like a bank hence the name. Any new process must declare the maximum number of instance of each resource type that it needs. It must not exceed the total resource.
Before allocating the system must make sure that after allocation it is not leaving the system in the unsafe state.
The data structures used in banker’s algorithm where ![]() is the number of processes and
is the number of processes and ![]() is the number of resource types is as follows,
is the number of resource types is as follows,
- Available – number of available resources of each type of length
 .
. ![Rendered by QuickLaTeX.com Available[j] = k](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-37c53f881dbb832f41bbff70ce44ebed_l3.png) means
means  instance of resource
instance of resource 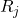 .
. - Max – It is
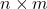 matrix for maximum number instance of resources required by the process.
matrix for maximum number instance of resources required by the process. ![Rendered by QuickLaTeX.com Max[i][j] = k](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-c8e1b9ee717f504be9a548311ab63e9d_l3.png) means
means 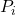 process requires
process requires 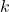 instance of resource
instance of resource 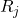 .
. - Allocation – it is also
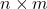 matrix for number of resources of each type allocated to each process.
matrix for number of resources of each type allocated to each process. ![Rendered by QuickLaTeX.com Allocation [i] [j] = k](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-38caa8783fbbf2ee8808a398b076397f_l3.png) means process
means process 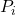 is allocated
is allocated 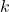 instances of resources of
instances of resources of 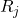 .
. - Need – it is
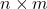 matrix that remaining need for each process.
matrix that remaining need for each process. ![Rendered by QuickLaTeX.com Need[i] [k] = k](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-03040c802283533ddf3783faaf78c735_l3.png) means that the process
means that the process 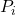 need
need 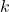 instance of resource type
instance of resource type 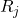 to finish its tasks.
to finish its tasks.
Need[i] [j] = Max[i] [j] – Allocation[i] [j]Banker’s Algorithm Procedure
If ![]() and
and ![]() are two vectors, then
are two vectors, then ![]() only if
only if ![]() for all
for all ![]() .
.
Conversely, ![]() if
if ![]() and
and ![]() .
.
![]() means resource currently allocated to process
means resource currently allocated to process ![]() and
and ![]() means additional resource required by process
means additional resource required by process ![]() .
.
Safety Algorithm
1. Let "Work" and "Finish" be two vectors of length m and n respectively.
2. Initialize Work = Available and Finish[i] = false, for i = 0, 1, 2, ..., n-1.
3. Find an index ‘i’ such that
4. Finish[i] = false
5. Need(i) <= Work
If no such ‘i’ exists, then go to step 3.
6. Work = Work + Allocation (i)
7. Finish[i] = true
8. Go to step 2.
If Finish[i] = true for all i then the system is in safe state.
Order of the above algorithm is ![]() .
.
Resource-Request Algorithm
This algorithm determines whether the request can be safely granted.
![]() is a request vector for process
is a request vector for process ![]() . If
. If ![]() , then process
, then process ![]() wants
wants ![]() instance of resource
instance of resource ![]() . When a request for a resource is made, following activities take place
. When a request for a resource is made, following activities take place
- If
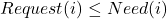 , go to step 2, otherwise raise error because process has exceeded its maximum claim.
, go to step 2, otherwise raise error because process has exceeded its maximum claim. - If
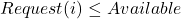 , go to step 3. Otherwise,
, go to step 3. Otherwise, 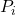 must wait, since the resources are not available.
must wait, since the resources are not available. - Let system pretend that it has allocated the resources to
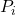 as follows
as follows
\begin{aligned}
&Available = Available – Request (i)\\
&Allocation (i) = Allocation (i) + Request (i)\\
&Need (i) = Need (i) – Request (i)
\end{aligned}If the resulting resource-allocation state is in a safe state, the transaction is completed and process ![]() gets the resource. If not, then
gets the resource. If not, then ![]() must wait, and old resource-allocation state is restored.
must wait, and old resource-allocation state is restored.
Example:
\begin{aligned}
&P = \{P0, P1, P2, P3, P4\}\\\\
&R = \{A, B, C\}
\end{aligned}Instances of Resources
A = 10, B = 5, C = 7
At ![]() time following snapshot of system is captured.
time following snapshot of system is captured.
| Allocation | Maximum | Available | |||||||
| A | B | C | A | B | C | A | B | C | |
| 0 | 1 | 0 | 7 | 5 | 3 | 7 | 5 | 5 | |
| 2 | 0 | 0 | 3 | 2 | 2 | 5 | 3 | 2 | |
| 3 | 0 | 2 | 9 | 0 | 2 | 10 | 5 | 7 | |
| 2 | 1 | 1 | 2 | 2 | 2 | 7 | 4 | 3 | |
| 0 | 0 | 2 | 4 | 3 | 3 | 7 | 4 | 5 |
We know that ![]()
| NEED Matrix | |||
| A | B | C | |
| 7 | 4 | 3 | |
| 1 | 2 | 2 | |
| 6 | 0 | 0 | |
| 0 | 1 | 1 | |
| 4 | 3 | 1 |
Check if the System is in Safe State
Iteration 1
Step 1:
\begin{aligned}
&Need (i) <= Available, \hspace{3px}if \hspace{3px} True then,\\\\
&Need (0) > Available => (7, 4, 3) > (3, 3, 2)\\\\
&Need (1) < Available => (1, 2, 2) < (3, 3, 2)
\end{aligned}Step 2:
\begin{aligned}
&Work = Work + Allocation (i)\\\\
&Work = (3, 3, 2) + (2, 0, 0) = (5, 3, 2)\\\\
&
\end{aligned}Step 3:
\begin{aligned}
&Add \hspace{3px}P_1 \hspace{3px}to \hspace{3px}Safety \hspace{3px}Sequence\\\\
&Safety \hspace{3px} sequence = \{P_1\}
\end{aligned}Iteration 2
Step 1:
\begin{aligned}
&Need (i) <= Available, \hspace{3px} if \hspace{3px} True \hspace{3px} then,\\\\
&Need (2) > Available => (6, 0, 0) > (5, 3, 2)\\\\
&Need (3) < Available => (0, 1, 1) < (5, 3, 2)\\\\
\end{aligned}Step 2:
\begin{aligned}
&Work = Work + Allocation (i)\\\\
&Work = (5, 3, 2) + (2, 1, 1) = (7, 4, 3)\\\\
\end{aligned}Step 3:
\begin{aligned}
&Add \hspace{3px} P_1 \hspace{3px} to \hspace{3px} Safety \hspace{3px}Sequence\\\\
&Safety \hspace{3px}sequence = \{P_1, P_3\}
\end{aligned}Iteration 3
Step 1:
\begin{aligned}
&Need (i) <= Available, \hspace{3px} if \hspace{3px}True \hspace{3px}then,\\\\
&Need (4) <= Available => (4, 3, 1) < (7, 4, 3)
\end{aligned}Step 2:
\begin{aligned}
&Work = Work + Allocation (i)\\\\
&Work = (7, 4, 3) + (0, 0, 2) = (7, 4, 5)
\end{aligned}Step 3:
\begin{aligned}
&Add \hspace{3px}P_1 \hspace{3px}to \hspace{3px}Safety \hspace{3px}Sequence\\\\
&Safety \hspace{3px}sequence = \{P_1, P_3, P_4\}
\end{aligned}Iteration 4
Step 1:
\begin{aligned}
&Need (i) <= Available, \hspace{4px} if \hspace{4px} True \hspace{4px} then,\\\\
&Need (0) <= Available => (7, 4, 3) < (7, 4, 5)\\\\
\end{aligned}Step 2:
\begin{aligned}
&Work = Work + Allocation (i)\\\\
&Work = (7, 4, 5) + (0, 1, 0) = (7, 5, 5)
\end{aligned}Step 3:
\begin{aligned}
&Add \hspace{3px}P_1 \hspace{3px}to \hspace{3px}safety \hspace{3px}sequence\\\\
&Safety \hspace{3px}sequence = {P1, P3, P4, P0}
\end{aligned}Iteration 5
Step 1:
\begin{aligned}
&Need (i) <= Available, \hspace{3px}if \hspace{3px}True \hspace{3px}then,\\\\
&Need (2) <= Available => (6, 0, 0) < (7, 5, 5)
\end{aligned}Step 2:
\begin{aligned}
&Work = Work + Allocation (i)\\\\
&Work = (7, 5, 5) + (3, 0, 2) = (10, 5, 7)
\end{aligned}Step 3:
\begin{aligned}
&Add \hspace{3px}P_1 \hspace{3px}safety \hspace{3px}sequence\\\\
&Safety \hspace{3px}sequence = \{P_1, P_3, P_4, P_0, P_2\}
\end{aligned}Handling a Request
Suppose process ![]() requested resource
requested resource ![]() which is less than the available resources
which is less than the available resources ![]() .
.
Request (i) <= Available => (1, 0, 2) < (3, 3, 2)
The system will pretend that the resource is allocated successfully but will run the Safety Algorithm demonstrated above and verify if whether allocation to ![]() will leave the system in an UNSAFE state.
will leave the system in an UNSAFE state.
Example:
Suppose ![]() requested for
requested for ![]() , then we find that
, then we find that ![]() Adjust the following
Adjust the following
\begin{aligned}
&Available:= Available - Request;\\\\
&Allocation; =Allocation +Request;;\\\\
&Need; =Need- Request;
\end{aligned}| Allocation | Maximum | Available | |||||||
| A | B | C | A | B | C | A | B | C | |
| 0 | 3 | 0 | 7 | 5 | 3 | 3,7 | 1,5 | 2,5 | |
| 2 | 0 | 0 | 3 | 2 | 2 | 5 | 1 | 2 | |
| 3 | 0 | 2 | 9 | 0 | 2 | ||||
| 2 | 1 | 1 | 2 | 2 | 2 | 7 | 2 | 3 | |
| 0 | 0 | 2 | 4 | 3 | 3 | 7 | 2 | 5 |
We then run the Safety Algorithm
| NEED Matrix | |||
| A | B | C | |
| 7 | 2 | 3 | |
| 1 | 2 | 2 | |
| 6 | 0 | 0 | |
| 0 | 1 | 1 | |
| 4 | 3 | 1 |
Iteration 1
Step 1:
\begin{aligned}
&Need (i) <= Available, \hspace{3px}if \hspace{3px}True \hspace{3px}then,\\\\
&Need (1) <= Available => (1, 2, 2) < (3, 1, 2)\\\\
\end{aligned}Step 2:
\begin{aligned}
&Work = Work + Allocation (i)\\\\
&Work = (3, 1, 2) + (2, 0, 0) = (5, 1, 2)
\end{aligned}Step 3:
\begin{aligned}
&Add \hspace{3px}P_1 \hspace{3px}to \hspace{3px} safety \hspace{3px}sequence\\\\
&Safety \hspace{3px} sequence = {P1}
\end{aligned}Iteration 2
Step 1:
\begin{aligned}
&Need (i) <= Available, \hspace{3px} if \hspace{3px}True \hspace{3px}then,\\\\
&Need (2) > Available => (6, 0, 0) > (5, 1, 2)\\\\
&Need (3) <= Available => (0, 1, 1) < (5, 1, 2)
\end{aligned}Step 2:
\begin{aligned}
&Work = Work + Allocation (i)\\\\
&Work = (5, 1, 2) + (2, 1, 1) = (7, 2, 3)
\end{aligned}Step 3:
\begin{aligned}
&Add \hspace{3px}P_3 \hspace{3px} to \hspace{3px} safety \hspace{3px} sequence\\\\
&Safety \hspace {3px} sequence = \{P_1, P_3\}
\end{aligned}Iteration 3
Step 1:
\begin{aligned}
&Need (i) <= Available, \hspace{3px}if \hspace{3px}True \hspace{3px} then,\\\\
&Need (4) <= Available => (4, 3, 1) < (7, 2, 3)\\\\\end{aligned}Step 2:
\begin{aligned}
&Work = Work + Allocation (i)\\\\
&Work = (7, 2, 3) + (0, 0, 2) = ( 7, 2, 5 )
\end{aligned}Step 3:
\begin{aligned}
&Add \hspace{3px} P_1 \hspace{3px} to \hspace{3px} safety \hspace{3px} sequence\\\\
&Safety \hspace{3px}sequence = \{P_1, P_3, P_4 = not \hspace{3px} safe\}
\end{aligned}References
- Abraham Silberschatz, Peter B. Galvin, Greg Gagne, A Silberschatz. 2012. Operating System Concepts, 9th Edition. Wiley.
