The C program to find permutation and combination solves 4 different types of problems. The permutation problems are arrangement problems and the combination problems are selection problems.
You will more details about each type of problem in the problem definition section.
The list of problems is given below
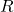-permutation of a set of 
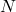distinct objects where 
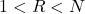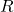.- -permutation of a set of 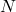distinct objects with repetition allowed.
- Permutation of 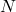objects where 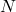is not distinct and contains indistinguishable objects of different types –
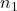types, 
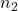types, 
,
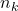types. 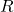- -combination of a set of 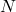distinct objects where .
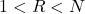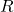- -combination of a set of 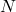distinct objects with repetition allowed.
You must be familiar with following concepts before learning from this examples.
Problem Definition: R-permutation of N distinct objects
A permutation is the number of arrangement of N distinct objects taken R at a time. Suppose we have N people sitting in a row of chairs, how many ways to change the sitting arrangement taken R people at a time.
For example, suppose we have 3 men sitting on 3 chairs; let’s call them A, B and C. The number of arrangements of 2 men out of 3 i.e., N =3, R = 2 is given below.
AB AC BC
BA CA CBIn the above example, the order of the arrangement matters and each of these different orders is counted
\begin{aligned}
& Formula for Permutation = \frac{N!}{(N-R)!}\\ \\
&nPr = n! / (n-r)!
\end{aligned}Flowchart 1 – Permutation without Repetition
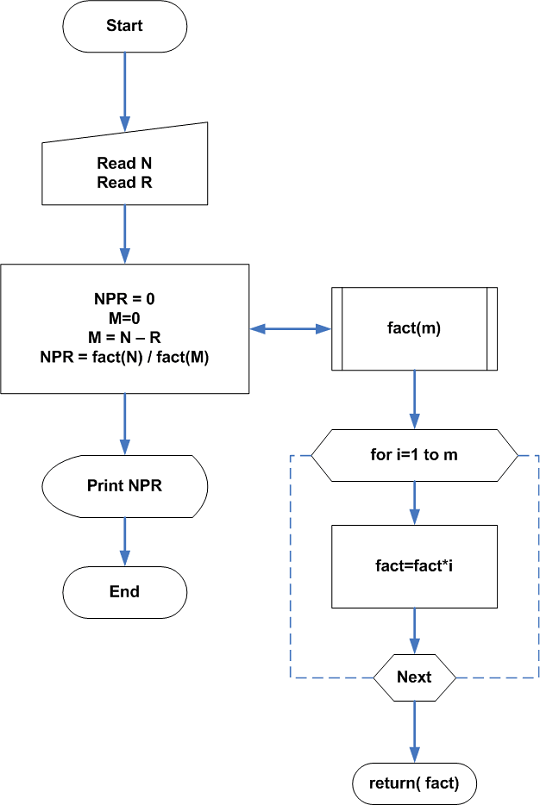
Program Code – Permutation No Repetition
The C program for the permutation of numbers is given below.
#include <stdio.h>
#include <conio.h>
int fact(int);
int main()
{
int NPR,N,R,M,i;
NPR=0;
M=0;
M= N-R;
printf("Enter value for N and R:");
scanf("%d %d",&N,&R);
NPR = fact(N)/fact(M);
for(i=0;i<45;i++)
printf("_");printf("\n\n");
printf("Number of %d-permutation of %d object
= %dn",R,N,NPR);
for(i=0;i<45;i++)
printf("_");printf("\n\n");
system("PAUSE");
return 0;
}
int fact(m)
{
int i,fact=1;
for(i=1;i<=m;i++)
{
fact=fact*i;
}
return(fact);
}Output
The output of the first program is given below.
Enter value for N and R: 10 2
------------------------------------------------
Number of 2-permutation of 10 objects = 3628800
------------------------------------------------Problem Definition: R-permutation of a set of N distinct objects with repetition allowed
In permutation without repetition, you select R objects at a time from N distinct objects. Now you have R positions to arrange N objects.
\begin{aligned}
&First \hspace{2px}position \hspace{2px}can \hspace{2px}have \hspace{2px} N \hspace{2px}choices.\\ \\
&The \hspace{2px}second\hspace{2px} position \hspace{2px}can \hspace{2px}have \hspace{2px}( N-1 ) \hspace{2px}choices.\\ \\
&The\hspace{2px} third \hspace{2px}position\hspace{2px} can \hspace{2px} have \hspace{2px}(N - 2) \hspace{2px}choices.\\ \\
&\cdots \\
&\cdots \\
&\cdots \\ \\
&R^{th} \hspace{2px}position \hspace{2px} can \hspace{2px} have \hspace{2px} ( N - R + 1 )\hspace{2px} choices.
\end{aligned}For example
\begin{aligned}&Let \hspace{2px} N = 6, R = 3\\ \\ &1^{st} \hspace{2px}Position \hspace{10px} 2^{nd} \hspace{2px} Position \hspace{10px} 3^{rd} \hspace{2px} Position\\ &6 \hspace{2px} choices \hspace{5px}\times \hspace{5px} 5 \hspace{2px} choices \hspace{5px}\times \hspace{5px}4 \hspace{2px} choices = 120 \end{aligned}However, with permutation with repetition allowed, the above example becomes
\begin{aligned}&1^{st} \hspace{2px}Position \hspace{10px} 2^{nd} \hspace{2px} Position \hspace{10px} 3^{rd} \hspace{2px} Position\\ &6 \hspace{2px} choices \hspace{5px}\times \hspace{5px} 6 \hspace{2px} choices \hspace{5px}\times \hspace{5px}6\hspace{2px} choices = 120 \end{aligned}In other words, the N objects are repeated R times 
.
Flowchart 2 – Permutation with repetition allowed
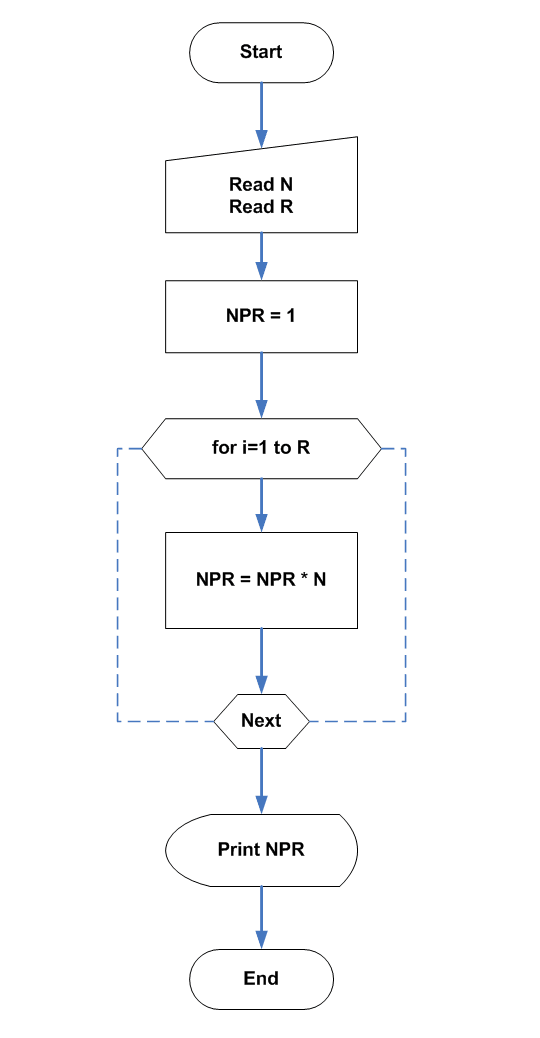
Program Code – Permutation with repetition allowed
The C program for permutation with repetition allowed is given below.
/* program to find npr = n^r */
#include <math.h>
#include <stdio.h>
#include <conio.h>
main()
{
int i,N,R,NPR;
NPR =1;
printf ("Enter the values for N and R:");
scanf ("%d %d", &N, &R);
for(i=0;i<R;i++)
{
NPR = NPR * N;
}
for(i=0;i<50;i++)
printf("_");printf("\n\n");
printf("Number of %d-permutation of %d with Repetition
= %d\n",R,N,NPR);
for(i=0;i<50;i++)
printf("_");printf("\n\n");
system("PAUSE");
return 0;
}Output 2
The output of the program for permutation with repetition allowed is given below.
Enter the values for N and R:5 4
--------------------------------------------------------------
Number of 4-permutation of 5 with Repetition = 625
--------------------------------------------------------------Problem Definition: Permutation of N objects where N is not distinct and contains indistinguishable objects
Another type of permutation problem is when you have object, but they are not distinct and contains many objects of similar types.
\begin{aligned}
&N \hspace{2px} objects = x \hspace{2px}object \hspace{2px}of \hspace{2px}n_1 \hspace{2px} type + \\\\
&y \hspace{2px} object \hspace{2px}of \hspace{2px}n_2 \hspace{2px}type + \\ \\
&z\hspace{2px} object \hspace{2px}of\hspace{2px} n_3 \hspace{2px}type + \\ \\
&\cdots + \\\\
&p \hspace{2px}objects \hspace{2px}of \hspace{2px}n_k \hspace{2px}type
\end{aligned}The formula is given by following
\begin{aligned} N = n_1 + n_2 + n_3 + \cdots + n_k\end{aligned}To find the permutation of N objects where some of them of indistinguishable, you use following.
\begin{aligned}nPr = \frac{ n! }{ (n_1! + n_2! + n_3!)}\end{aligned}Flowchart 3 – Permutation of Indistinguishable Objects
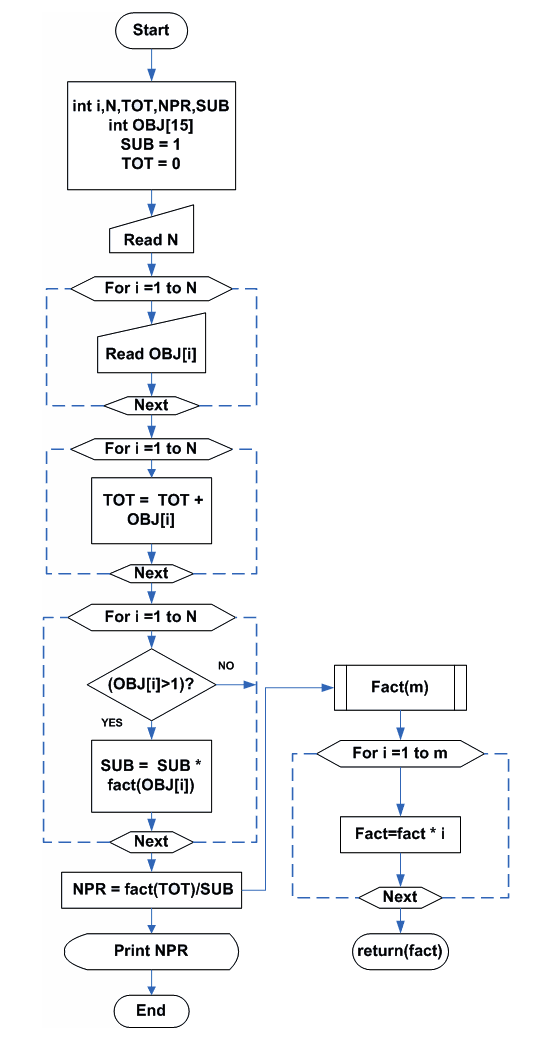
Program Code – Permutation of Indistinguishable Objects
The C program for the permutation of numbers where some objects are indistinguishable.
#include <stdio.h>
#include <conio.h>
#include<math.h>
int fact(int);
main()
{
int i,N,TOT,NPR,SUB;
int OBJ[15];
SUB = 1;TOT = 0;
printf ("Enter the values for number of object N:");
scanf("%d",&N);
for(i=1;i<=N;i++)
{
printf("How many number of object OBJ[%d]?:",i);
scanf ("%d", &OBJ[i]);
}
for(i=1;i<=N;i++)
{
TOT = TOT + OBJ[i];
}
for(i=1;i<=N;i++) {
if(OBJ[i]>1)
SUB = SUB * fact(OBJ[i]);
}
NPR = fact(TOT)/SUB;
for(i=0;i<50;i++)
printf("_");
printf("\n\n");
printf("Permutation of %d distinguishable objects
= %d\n",N,NPR);
for(i=0;i<50;i++)
printf("_");printf("\n\n");
system("PAUSE");
return 0;
}
int fact(m)
{
int i,fact=1;
for(i=1;i<=m;i++)
{
fact=fact*i;
}
return(fact);
}Output 3
The output of the program with permutation is given below.
Enter the values of number of object N:4
How many number of object OBJ[1]?:3
How many number of object OBJ[2]?:2
How many number of object OBJ[3]?:1
How many number of object OBJ[4]?:1
------------------------------------------------------
Permutation of 4 distinguishable objects = 420
------------------------------------------------------Problem Definition: R-combination of a set of N distinct objects
A combination is a selection of N distinct object taken R at a time. The word “Selection” is very important because it indicates that only a particular order of R objects is accepted.
For example, consider our example of permutation of A, B, and C.
AB AC BC
BA CA CBHere only one of the arrangement is “selected”, you can only select AB or BA, not both. This is called a Combination.
The formula for nCr is given below.
\begin{aligned}&Formula \hspace{2px} for \hspace{2px} Combination = \frac{N \hspace{2px} factorial }{ (R \hspace{2px} factorial \cdot (N-R) \hspace{2px} factorial)}\\ \\
&nCr = \frac{n!}{(r! \cdot (n-r)!)}
\end{aligned}Flowchart 4 – Combination No Repetition
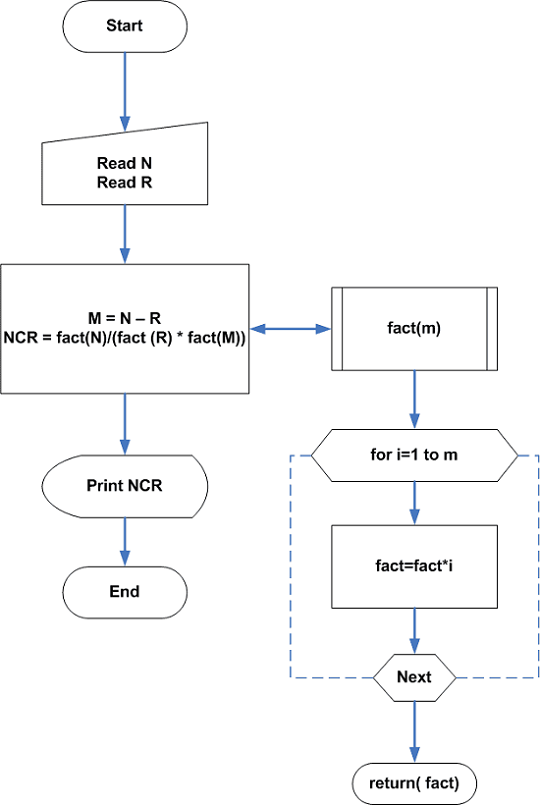
Program Code – Combination No Repetition
C program for the combination of numbers is given below.
/* program to find nCr */
#include <stdio.h>
#include <conio.h>
long int fact(long int);
int main()
{
long int i,N,R,M,NCR;
printf ("Enter the values for N and R: ");
scanf ("%d %d", &N, &R);
M = N - R;
NCR = fact(N)/(fact (R) * fact(M)); //ncr formula
for(i=0;i<45;i++)
printf("_");printf("\n\n");
printf("Number of %d-combination of %d
= %dn",R,N,NCR);
for(i=0;i<45;i++)
printf("_");printf("\n\n");
system("PAUSE");
return 0;
}
long int fact(long int m)
{
long int i,fact=1;
for(i=1;i<=m;i++)
{
fact=fact*i;
}
return(fact);
}Output 4
The output of the program is given below.
Enter the values for N and R: 10 5
---------------------------------------------
Number of 5-combination of 10 = 252
---------------------------------------------Problem Definition: R-combinations of a set of N distinct object with repetition allowed
We know that -combination is a selection of objects at a time from given object set. The -combination of a set of distinct object with repetition means that we can now select each object in more than once.
For example, Let’s 
, with 
and 
, and 
You need to select 2 object combination out of 3 such that you can now choose any object more than once.
AA AB AC BB BC CCThe formula for R-combination with repetition is given below.
formula with repetition
\begin{aligned}nCr = \frac{(n + r - 1)}{ ( r! \cdot (n - 1)!)}\end{aligned}The solution to the above problem is
4 2 * 3 * 2 * 1 / 2 * 1 * 2 * 1 = 6
Flowchart 5 – Combination with Repetition Allowed
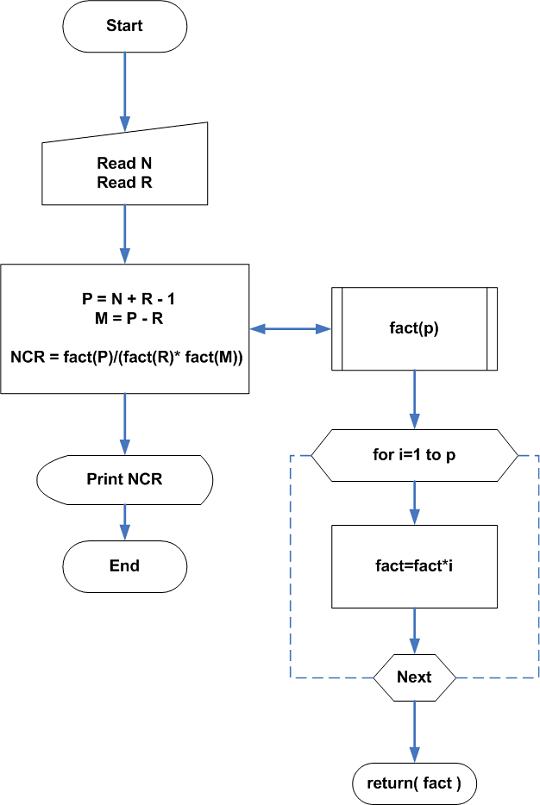
Program Code – Combination with Repetition Allowed
The C program for the combination of numbers with repetition allowed is given below.
/* program to find nCr with repetition */
#include <stdio.h>
#include <conio.h>
int main()
{
int N,R,P,M,fact(int);
int i,NCR;
printf ("Enter the value for N and R: ");
scanf ("%d %d", &N, &R);
P = N + R - 1;
M = P - R;
NCR = fact(P)/(fact(R)* fact(M));
for(i=0;i<45;i++)
printf("_");printf("\n\n");
printf("Number of %d-Combination of %d with Repetition
= %d\n",R,N,NCR);
for(i=0;i<45;i++)
printf("_");printf("\n\n");
system("PAUSE");
return 0;
}
int fact(p)
{
int i,fact=1;
for(i=1;i<=p;i++)
{
fact=fact*i;
}
return(fact);
}Output 5
The output of the program is given below.
Enter the value for N and R: 4 6
---------------------------------------------------
Number of 6-Combination of 4 = 84
---------------------------------------------------