C Program To Compute Nth Factorial Using Recursion

by

The program to compute factorial calls a function recursively to compute the output.The recursion is the ability of a computing procedure to call itself repeatedly until the problem is solved.

Advertisements

We compiled the program using Dev C++ version 5 (beta) compiler installed on Windows 7 64-bit system. You can use any standard C compiler, but make sure to change the source code according to compiler specifications.

You must know the following c programming concepts before trying the example program.

Problem Definition

In simple words, the factorial of a given number n is the product of all the numbers up to that number, including the number.

So factorial of 5 is 1 \times 2 \times 3 \times 4 \times 5 = 120

Advertisements

In the previous section, we introduced you to the concept of recursion. To elaborate on that see the example below. If factorial () is a function then,

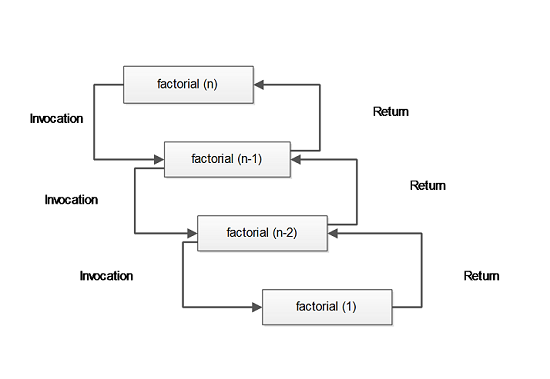
Recursion
Figure 1 – Recursion

Every time factorial function calls itself, it reduces 1 from the parameter of the function until the factorial(1) is reached. Then it starts processing or working from factorial(1) to the top – factorial(n) and prints the final results.

Flowchart – Factorial with Recursion

Flowchart - Factorial with Recursion
Figure 2 – Flowchart – Factorial with Recursion

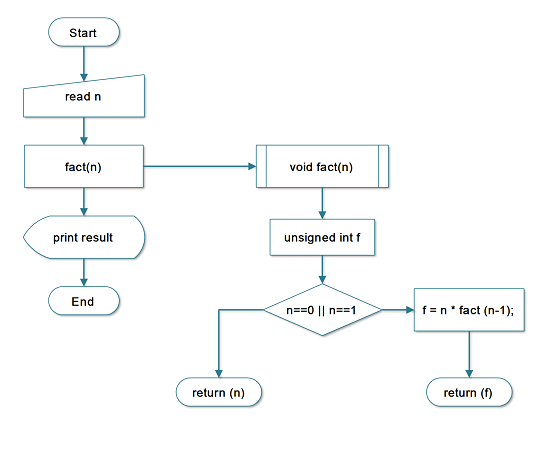
Program Code – Factorial with Recursion

/*Program to compute Nth factorial */
#include < stdio.h >
#include < stdlib.h >
int fact (int n)
{
    unsigned int f;
    if ((n == 0) || (n == 1))
        return (n);
    else
        /* Compute factorial by Recursive calls */
        f = n * fact (n - 1); 
        return (f);
}
main ()
{
    int i, n;
    /* Reading the number */
    printf ("Enter the Number :");
    scanf ("%d", & n);
    /* Printing results */
    for (i = 0; i < 30; i++)
    printf ("_");printf ("\n\n");
    printf ("Factorial of Number %d is %d\n", n, fact (n));
    for (i = 0; i < 30; i++)
    printf ("_");printf ("\n\n");
    system ("PAUSE");
    return 0;
}

The most important line of code in the above source code is following.

f = n * fact(n-1);

The n is the current number being multiplied and function fact(n-1) calls the previous number and this process continues till 1 reached. Then, the actual multiplication starts from fact(1) up to fact(n) processing all numbers and resulting in final output.

Output

                Enter the Number:5
                _______________________________
                Factorial of Number 5 is 120
                _______________________________

Advertisements