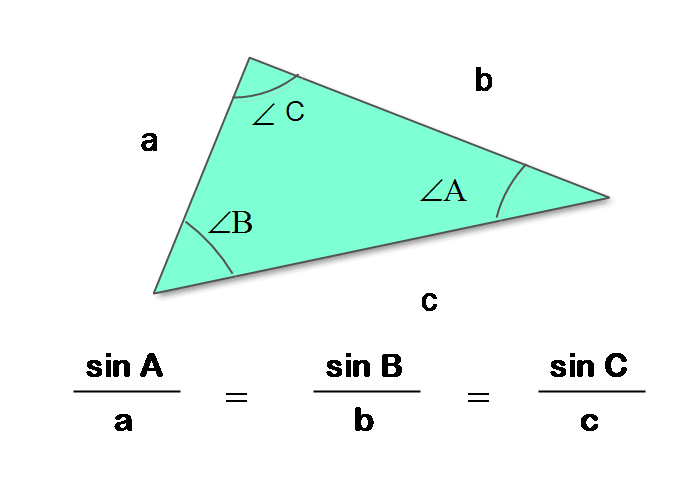
With the law of sine, you can find any unknown angle of a given triangle or the length of a particular side of a triangle or the length of a particular side of a triangle. This is a fundamental concept of trigonometry.
We used Dev-C++ to compile the program, but you may use any other standard C compiler. This program make use of math header – math.h especially, two trig functions – sin () function and asin () function at lot. So if you are choosing a different compiler then use the correct math header file.
Before you try the example, learn following C programming concepts. You can skip it if already know it well.
Problem Definition
The law of sine is given below. The triangle has three sides and
; It also has three angles –
and
.
In general, there are two cases for problems involving the law of sine.
Case 1: When the length of two sides is given and the angle opposite to one of the sides with length is given.
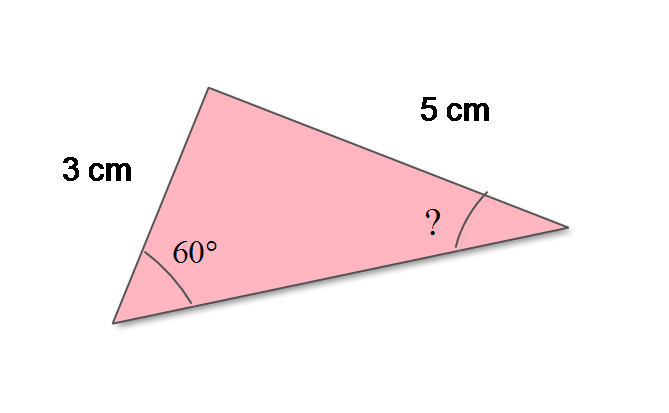
When the length of two side – and
are given and the angle opposite to side
is given. Then using law of sine
\begin{aligned}&X \hspace{1ex} = \hspace{1ex} sin \hspace{1ex} \frac{A}{a}\\ \\
&sin \hspace{1ex}\frac{B}{b} \hspace{1ex} = \hspace{1ex} X\\ \\
&sin \hspace{1ex} B \hspace{1ex} =\hspace{1ex} X \hspace{1ex}\ast \hspace{1ex}b\\ \\
&\angle {B }\hspace{1ex} = \hspace{1ex} arcsin ( X \ast b)
\end{aligned}This the way to find the value of sin and then using arcsin to find the
.
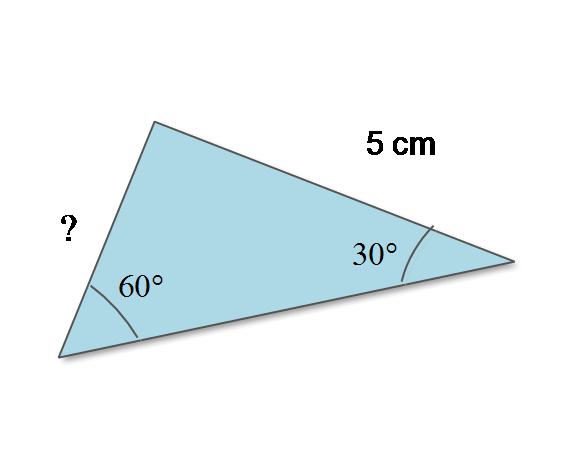
Case 2: When 2 angles – angle A and angle B are given with length of the side opposite to angle A or angle B.
When two angles and length of at least one side opposite to or
is given. Find the
and
values first.
Find or
, whichever is given in the problem.
The length of side
\begin{aligned}b \hspace{1ex} = \hspace{1ex} sin\hspace{2px} B \cdot X\end{aligned}This is how you will find the value of the length of side when
and
is given along with the length of side
.
In next section, you will find the flowchart of the program for the law of sine and the above two cases to understand the logic of the program.
Flowchart – Program for Law of Sine Problems
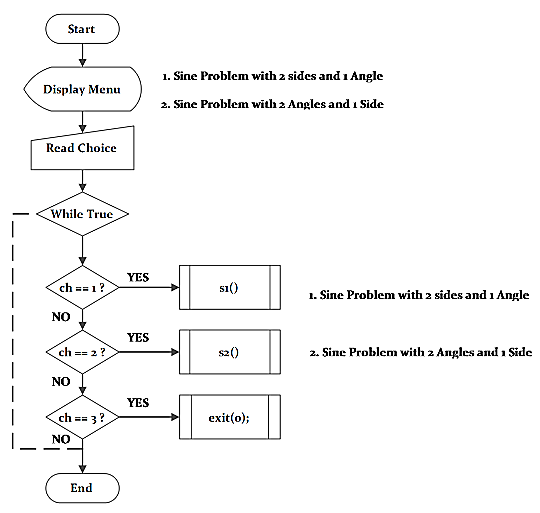
The next flowchart is of function which covers the case 1 of the law of sine problems.
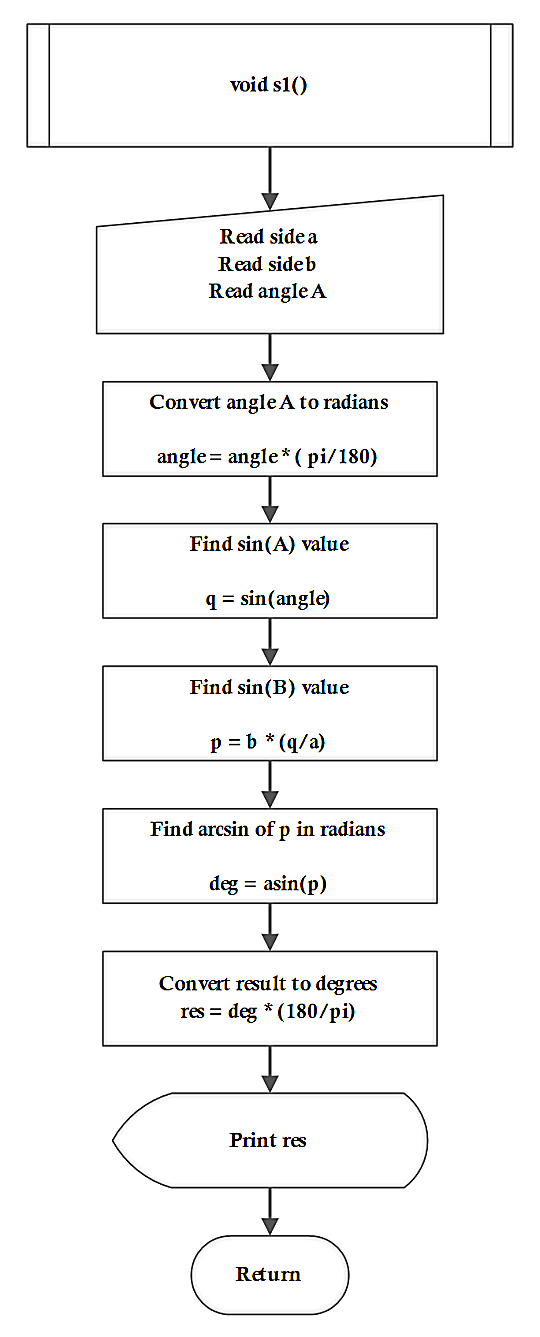
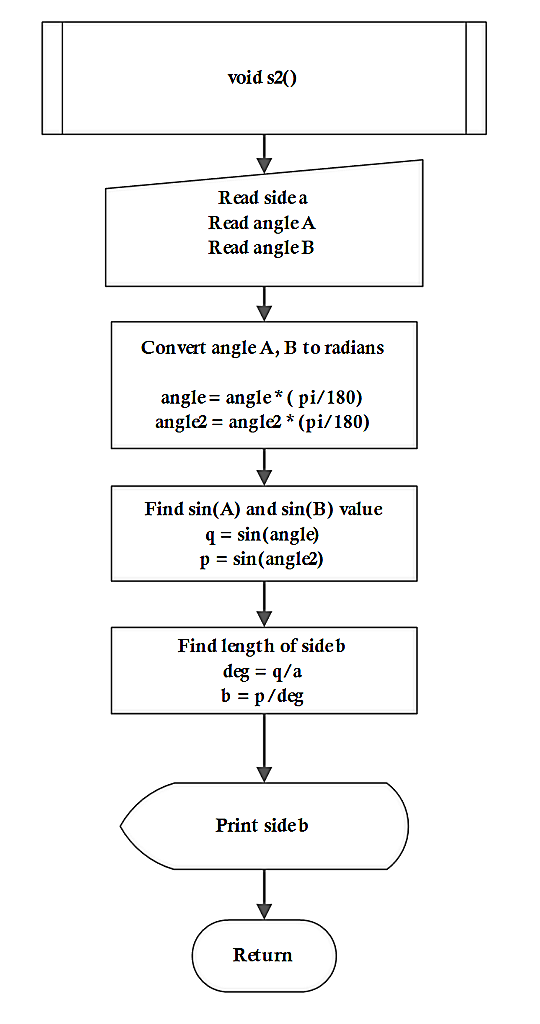
The flowchart for function that covers the case 2 of the law of sine problems is given below.
Program Code – Program for Law of Sine Problems
/* C Program for solving law of sine problems */
#include <stdio.h>
#include <math.h>
#include<stdlib.h>
/* Variable declarations */
int ch,i;
float a, b, q, p, deg;
float angle,angle2, res;
/* Function declaration */
void s1();
void s2();
int main()
{
for(i=0;i < 30;i++)
printf("*");printf("\n\n");
printf("\tMenu\n\n");
for(i=0;i < 30;i++)
printf("*");printf("\n\n");
printf("1.Sine Problem with 2 Sides and 1 Angle:\n");
printf("2.Sine Problem with 2 Angles and 1 Side:\n");
printf("3.Quit using any other number:\n\n");
for(i=0;i < 30;i++)
printf("*");printf("\n\n");
while(1)
{
printf("Enter your Choice:");
scanf("%d",& ch);
if(ch == 1)
{
s1();
}
else if(ch == 2)
{
s2();
}
else if(ch == 3)
{
exit(0);
}
else
{
printf("Wrong choice ! Try again:\n");
}
}
system("PAUSE");
return 0;
}
/* Main function ends */
/* Function definition - s1() */
void s1()
{
float pi = 3.141;
for(i=0;i < 30;i++)
printf("_");printf("\n\n");
printf("Enter value for side with angle:");
scanf("%f",&a);
printf("Enter value for side without angle:");
scanf("%f",&b);
printf("Enter the angle(degrees):");
scanf("%f",&angle);
for(i=0;i < 30;i++)
printf("_");printf("\n\n");
angle = angle * (pi/180);
q = sin(angle);
p = b * (q/a);
deg = asin(p);
res = deg * (180/pi);
for(i=0;i < 30;i++)
printf("_");printf("\n\n");
printf("Angle B = %f\n",res);
for(i=0;i < 30;i++)
printf("_");printf("\n\n");
}
/* Function definition - s2() */
void s2()
{
float pi = 3.141;
for(i=0;i < 30;i++)
printf("_");printf("\n\n");
printf("Enter value of side a with angle:");
scanf("%f",&a);
printf("Enter angle A for side a:");
scanf("%f",&angle);
printf("Enter value angle B of side b:");
scanf("%f",&angle2);
for(i=0;i < 30;i++)
printf("_");printf("\n\n");
angle = angle * (pi/180);
angle2 = angle2 * (pi/180);
q = sin(angle);
p = sin(angle2);
deg = q/a;
b = p/deg;
for(i=0;i < 30;i++)
printf("_");printf("\n\n");
printf("Side b = %f\n",b);
for(i=0;i<30;i++)
printf("_");printf("\n\n");
}Outputs from the Program
The program gives three choices during run time
- Apply the law of sine when the length of 2 sides and 1 angle opposite to a given side is available.
- Apply the law of sine when 2 angles are given and length of 1 side opposite to an angle is given.
- Quit the program
The output from both the cases are given below, you should run the program and verify the output for yourself.
Menu
***********************************************************************
1.Sine Problem with 2 Sides and 1 Angle:
2.Sine Problem with 2 Angles and 1 Side:
3.Quit using any other number:
***********************************************************************
Enter your Choice:1
_______________________________________________________________________
Enter value for side with angle:5
Enter value for side without angle:4
Enter the angle(degrees):60
_______________________________________________________________________
_______________________________________________________________________
Angle B = 43.855770
_______________________________________________________________________
Enter your Choice:_Now, we will test option 2 from the menu.
Menu
***********************************************************************
1.Sine Problem with 2 Sides and 1 Angle:
2.Sine Problem with 2 Angles and 1 Side:
3.Quit using any other number:
***********************************************************************
Enter your Choice:2
_______________________________________________________________________
Enter value of side a with angle:30
Enter angle A for side a:14
Enter value angle B of side b:55
_______________________________________________________________________
_______________________________________________________________________
Side b = 101.586449
_______________________________________________________________________
Enter your Choice:_