Skip to content
Home » C Program for Tower of Hanoi Problem using Recursion

C Program for Tower of Hanoi Problem using Recursion

    The Tower of Hanoi is an interesting recurrence relation problem. In this example, you will write a program to solve the Tower of Hanoi using a recursive function.

    Before you begin, learn basics of C programming language, if you the basics skip this step and continue reading.

    Problem Definition

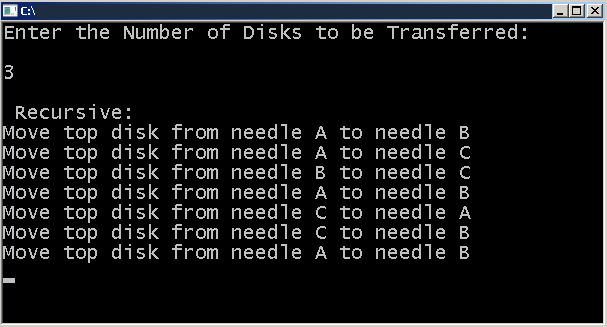
    Suppose you are given 3 disks of different size and 3 pegs. Each peg is labeled – A, B and C and smaller disk is always place on top of larger disks. The peg A has all three disks and your task is to move all the disks to the peg C. But there are rules to move disk between pegs.

    1. You can move only one disk at a time.
    2. You cannot place a larger disk on top of smaller disk.
    3. You should solve the problem with minimum disk movements.

    If the solution is achieved in 10 steps, a 12 step solution is not acceptable by rule 3.

    Learn more about Tower of Hanoi in the following article.

    Tower of Hanoi

    In this example, a recursive method is used to solve the Tower of Hanoi problem.

    Program Source Code

    #include <stdio.h>
#include <stdlib.h>

void hanoirecursion(int num,char ndl1, char ndl2, char ndl3)
{
    if(num == 1)
    {
    printf("Move top disk from needle %c to needle %c\n",ndl1,ndl2);
    return;
    }

hanoirecursion(num-1,ndl1,ndl3,ndl2);
printf("Move top disk from needle %c to needle %c\n",ndl1,ndl2);
hanoirecursion(num-1,ndl3,ndl2,ndl1);

}

int main()
{
    int no;
    printf("Enter the Number of Disks to be Transferred:\n\n");
    scanf("%d",&no);

if(no<1)
{
    printf("\n There is nothing to move:\n");
}
else
{
    printf("\n Recursive:\n");
    hanoirecursion(no,'A','B','C'); 
}

getch();
return 0;
}

    Output

    Output - Tower of Hanoi with Recursion
    Output – Tower of Hanoi with Recursion

    Related Articles: –