Previously, you learned about deriving an augmented matrix from a system of linear equations. You have also learned about reducing the augmented matrix into a simpler equivalent matrix that is easy to solve through series of row operations on the matrix. This kind of matrix form is known as the row echelon form of matrix.
Our goal for performing row operations on the matrix is to obtain the row echelon form or a reduced row echelon form from which deriving a solution to the system of linear equation is easy.
What is a Row Echelon Form of Matrix ?
The form of matrix that has following properties is said to be in row echelon form.
- Rows with all 0s are pushed to the bottom of the matrix.
- A row with first non-zero value as 1 is called leading 1.
- The leading 1 in the lower row is to the farthest right than the leading 1 at row above it.
- All other entries in the row except the last column as zero.
We now discuss each of the above points to explain the row echelon form.
Row with all zeros are pushed to the bottom
Suppose we are given a system of linear equations as follows.
\begin{aligned}
&0x + 0y + 0z = 0\\
&2x + y + 2z = 10\\
&0x + 0y + 0z = 0\\
&x - 2y + z = 2
\end{aligned}The augmented matrix that we derived is given below.
\begin{aligned}
&A = \begin{bmatrix}0 & 0 & 0 & 0 \\2 & 1 & 2 & 10 \\0 & 0 & 0 & 0 \\1 & -2 & 1 & 2\end{bmatrix}
\end{aligned}Since, row that only zero does not give any proper solution to the system of equation it is of no use and pushed to the bottom of the matrix or eliminated subsequently.
\begin{aligned}
&A = \begin{bmatrix}2 & 1 & 2 & 10 \\1 & -2 & 1 & 2\\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}
\end{aligned}First non-zero value must be a 1
The first non-zero value of each row in echelon form must be a 1 called the leading 1. Consider following example,
\begin{aligned}
&A = \begin{bmatrix}0 & 1 & 0 & 2 \\1 & 0 & 0 & 1\\0 & 0 & 1 & 3 \end{bmatrix}
\end{aligned}In the matrix above first non-zero element is a 1. Such a form is possible by a series of row operations on the original augmented matrix.
Leading 1 of lower row is to the farthest right than the row above
If you look at the previous, the matrix is still not in the echelon form because middle row has leading to the left than the leading 1 of the first row.
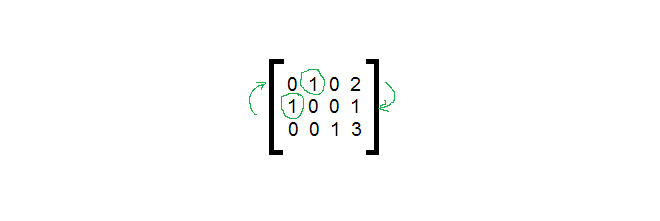
The leading 1 of the top row is to the right of the leading 1 of the the bottom row. To solve the problem, we do a row exchange between first and the second row. The result is in a row echelon form.
\begin{aligned}
&A = \begin{bmatrix}1 & 0 & 0 & 1 \\0 & 1 & 0 & 2 \\0 & 0 & 1 & 3 \end{bmatrix}
\end{aligned}All other entries must be zero except the last column
Only if the other entries are zero, we could use back substitution for obtaining a solution to the matrix. The last column is not zero because it is part of the solution and we obtain the value of unknown from it. We will discuss about back substitution when we discuss about Gauss-Jordan elimination method for finding solution to the system of linear equations.
Difference Between Row Echelon Form and Reduced Row Echelon Form
In the row echelon form, the lower triangular matrix below the leading 1 is zero, whereas reduced row echelon form has both upper triangular and lower triangular values as zero with leading 1.
Row Echelon Example
\begin{aligned}
A = \begin{bmatrix}1 & 0 & 3 & 1 \\0 & 1 & 5 & 2 \\0 & 0 & 1 & 3 \end{bmatrix}
\end{aligned}Reduced Row Echelon Form Example
\begin{aligned}
A = \begin{bmatrix}1 & 0 & 0 & 1 \\0 & 1 & 0 & 2 \\0 & 0 & 1 & 3 \end{bmatrix}
\end{aligned}In a system of equations, there can be more than one row echelon form, however, there is only one reduced row echelon form of the matrix.
