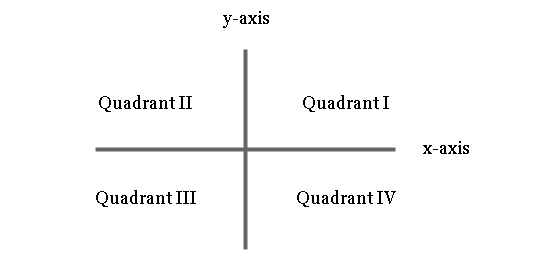
Cartesian plane is a two dimensional co-ordinate system. This system has two axis – the x-axis and the y-axis. The center of the Cartesian plane is called the origin.
The x-axis and the y-axis divide the plane into 4 different quadrants as shown in the figure above. The axis are real number line with 0 at the origin.
Any point on the plane is plotted in terms of horizontal distance on x-axis and vertical distance on y-axis.
p = (x, y)
where 
is distance on x-axis and is distance on y-axis.
Example: Plot a point for 
.
Solution:
\begin{aligned}&if \hspace{2px} p = (3, 5) \hspace{2px} then\\ \\
&x = 3\\ \\
&y = 5
\end{aligned}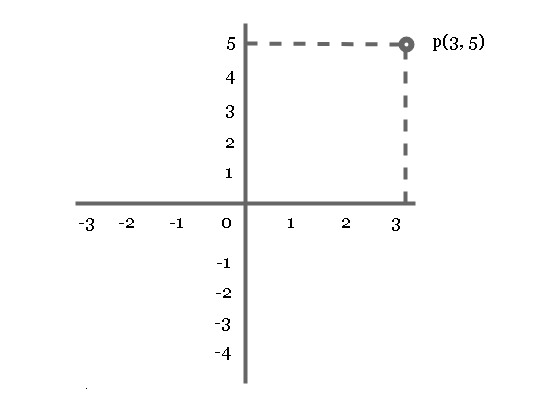
Pythagorean Theorem and Distance Formula
Pythagorean theorem is used for finding the distance of hypotenuse of a right triangle. The formula is modified to find the distance of two point on the Cartesian plane.
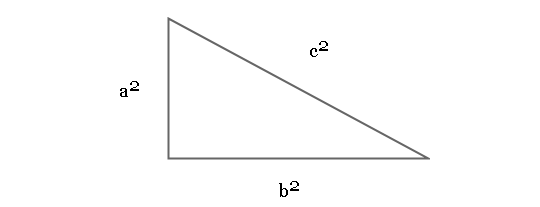
The above triangle has three sides – a, b and c, then Pythagorean theorem is given by
\begin{aligned}
&a^2 + b^2 = c^2\\ \\
&c = \sqrt{a^2 + b^2}
\end{aligned}Suppose there are two points on the Cartesian plane.
\begin{aligned}
&p(x_1, y_1) = (2, 4)\\ \\
&q(x_2, y_2) = (2. 2)
\end{aligned}and we have to find the distance between them.
Using Pythagorean theorem, we get
a = | y2 – y1 | = length of a
b = | x2 – x1 | = length of b
Therefore,
Distance formula for two points is
\begin{aligned}
&d = \sqrt{(|x2 - x1|)^2 +(|y2 - y1|)^2}\\ \\\
&d = \sqrt{(|2 - 2|)^2 +(|2 - 4|)^2}\\ \\
&d = \sqrt{(0)^2 + (-2)^2}\\ \\
&d = 2
\end{aligned}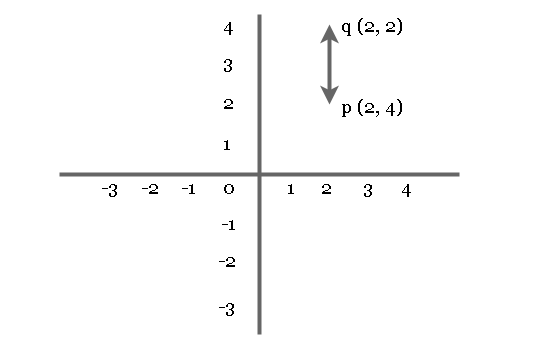
The above diagram verify the results and it shows that the distance is actually 2 units. Hence, the distance formula is correct and applies to the Cartesian plane.
