In the previous article, you learned about composite function, in this article, you will learn about inverse functions. The term “inverse” means to “undo” something and which is what the “inverse” of a function do. If a function ![]() find the
find the ![]() value for an
value for an ![]() value, the inverse of the function does the opposite, meaning it finds the
value, the inverse of the function does the opposite, meaning it finds the ![]() value for a given
value for a given ![]() value.
value.
Function and its inverse
Remember from previous articles, that the function ![]() is set of ordered pair
is set of ordered pair ![]() , that is, for every input
, that is, for every input ![]() there is a one and only
there is a one and only ![]() .
.
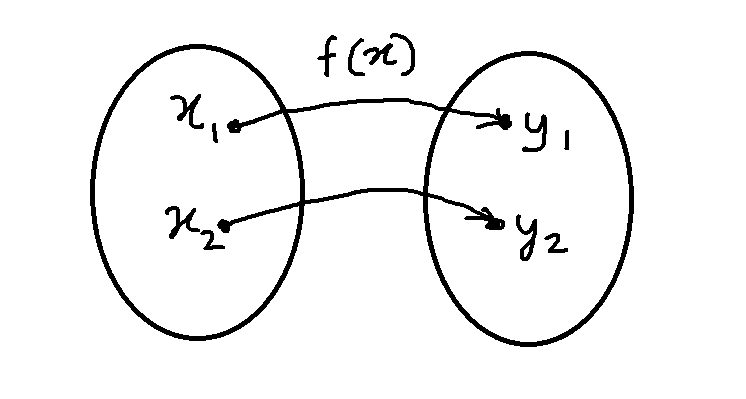
Suppose ![]() is function that takes input
is function that takes input ![]() and gives us the value
and gives us the value ![]() . We are just undoing the function
. We are just undoing the function ![]() . Therefore, if
. Therefore, if ![]() is inverse function of
is inverse function of ![]() , then it is denoted as
, then it is denoted as ![]() .
.
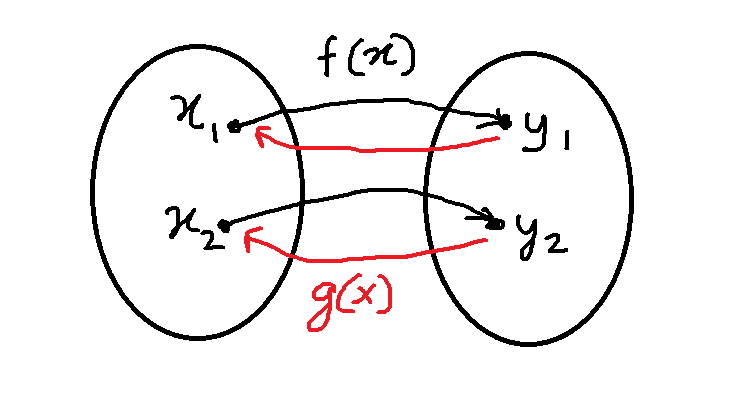
The inverse of the function ![]() is the set of ordered pairs
is the set of ordered pairs ![]() .
.
One-To-One Relationship
If you look at the figure 2, you will find that there is a one-to-one relationship between function ![]() and its inverse
and its inverse ![]() .
.
If there are two functions ![]() and its inverse function
and its inverse function ![]() , then
, then
![]()
Where ![]() is all values in the domain of inverse function
is all values in the domain of inverse function ![]() . Similarly,
. Similarly,
![]()
Where ![]() is all values in the domain of function
is all values in the domain of function ![]() .
.
If a function ![]() does not maintain the one-to-one relationship, there is no inverse. Consider the quadratic function
does not maintain the one-to-one relationship, there is no inverse. Consider the quadratic function ![]() . The function has same outputs for
. The function has same outputs for ![]() and
and ![]() .
.
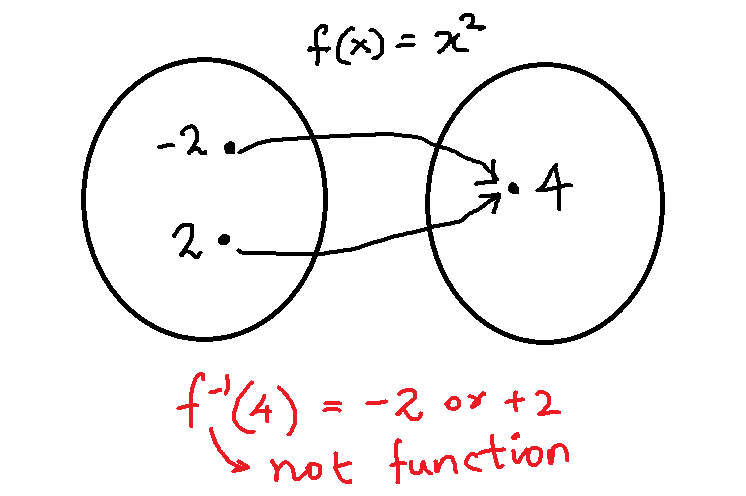
If we take an inverse of the function which is ![]() implies that there are two values for
implies that there are two values for ![]() . Therefore, inverse is not a function because a function can only have one output for given input
. Therefore, inverse is not a function because a function can only have one output for given input ![]() .
.
Horizontal Line Test
The easiest way to understand whether a function has inverse or not is to perform a horizontal line test on the graph of the function. To understand this concept , we will use our previous example of quadratic function ![]() . The graph of function is given below.
. The graph of function is given below.
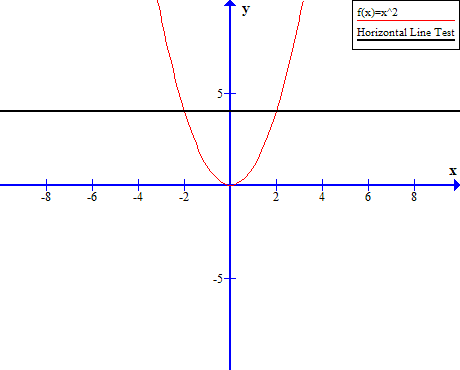
We perform a horizontal line test , that is, draw a horizontal line and if the line intersect the graph of function ![]() it has no inverse function. The figure 4 above, shows that the horizontal line intersect the graph of parabola, at
it has no inverse function. The figure 4 above, shows that the horizontal line intersect the graph of parabola, at ![]() and
and ![]() . Therefore,
. Therefore, ![]() has no inverse.
has no inverse.
Graph of Inverse Function
The graph of inverse function, if exists, can be obtained easily by changing the set of ordered pair ![]() to the set of ordered pair
to the set of ordered pair ![]() .
.
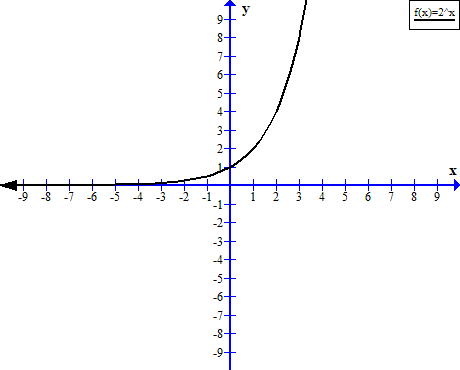
For example, consider the graph of exponential function ![]() which is an exponential function. The function passes the horizontal line test, therefore, an inverse function exists.
which is an exponential function. The function passes the horizontal line test, therefore, an inverse function exists.
| x | f(x) =2^x |
| -4 | 0.0625 |
| -3 | 0.125 |
| -2 | 0.25 |
| -1 | 0.5 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
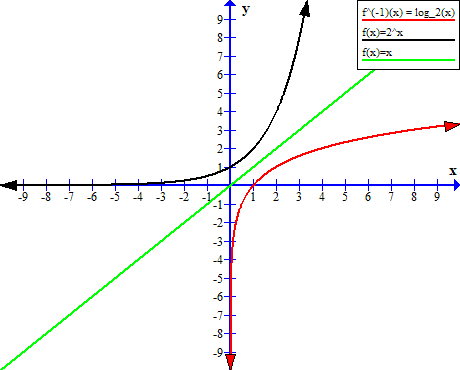
The inverse function is set of all ordered pairs ![]() . The inverse function of exponential function is
. The inverse function of exponential function is ![]() .
.
| x | f^{-1}(x) |
| 0.0625 | -4 |
| 0.125 | -3 |
| 0.25 | -2 |
| 0.5 | -1 |
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
Note that the inverse function is accepting all positive ![]() values, and all inverse function (shown in red) will reflect over the line ( in green)
values, and all inverse function (shown in red) will reflect over the line ( in green) ![]() . The ordered pairs
. The ordered pairs ![]() in exponential function is replaced with ordered pair
in exponential function is replaced with ordered pair ![]() .
.
How To Find The Inverse Function ?
To find the inverse of the function you must follow the following steps. If ![]() is a function with an expression, then
is a function with an expression, then
- Write
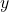 instead of
instead of 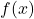 .
. - Interchange the
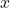 and
and 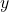 in the equation.
in the equation. - Solve the equation for
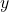 and if the equation does not define
and if the equation does not define 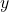 in terms of
in terms of 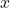 , then there is no inverse. Otherwise, you will have an equation that defines
, then there is no inverse. Otherwise, you will have an equation that defines 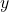 in terms of
in terms of 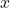 .
. - Replace
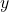 with
with 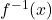 .
.
Now, it is necessary to verify the inverse function, that can be done by verifying ![]() and
and ![]() . The composition of
. The composition of ![]() and
and ![]() is an algebraic proof of inverse function.
is an algebraic proof of inverse function.
Example #1
Find the inverse function of ![]() .
.
Solution:
The given equation is ![]() . exponential equation and we expect to find a logarithmic function as inverse. But, we will go through all the steps to find the inverse of this function.
. exponential equation and we expect to find a logarithmic function as inverse. But, we will go through all the steps to find the inverse of this function.

Now , we must verify if the inverse function is correct, by using composition of functions. Therefore,
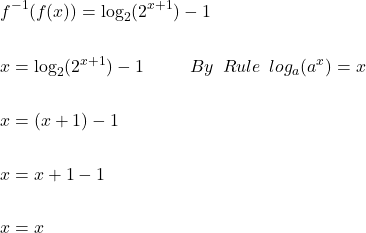
Similarly,
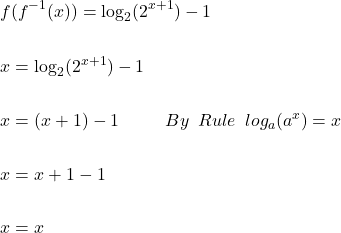
Example #2
Find the inverse function of the function ![]() .
.
Solution:
The function ![]() is a linear function. Therefore, an inverse function exists, but we will verify whether inverse exist of not by following our steps to find the inverse of a function.
is a linear function. Therefore, an inverse function exists, but we will verify whether inverse exist of not by following our steps to find the inverse of a function.
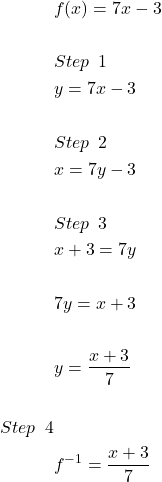
Now, we must verify the inverse function.
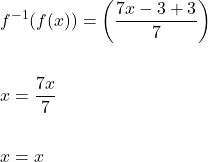
Similarly,
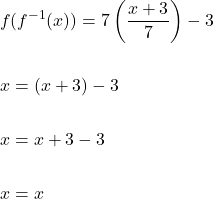
Restricted Domain
It is possible to find an inverse function to functions that does not have any inverse if we restrict the domain. It means we only accept set of ordered pairs ![]() of function
of function ![]() for which there exist ordered pairs
for which there exist ordered pairs ![]() .
.
Consider the graph of absolute value function [latedpage]![]() . This graph did not pass the horizontal line test and for each
. This graph did not pass the horizontal line test and for each ![]() value, there exist two
value, there exist two ![]() values.
values.
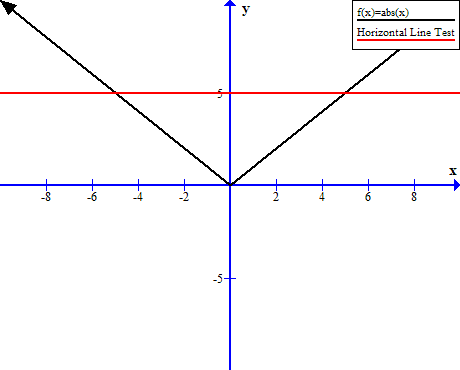
The graph will pass the horizontal line test if we restrict the domain to ![]() , therefore, an inverse of absolute value function exists if we choose values between the interval
, therefore, an inverse of absolute value function exists if we choose values between the interval ![]() .
.
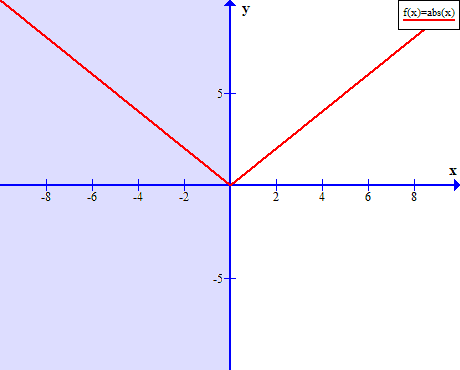
The inverse of the new restricted absolute function is as follows.
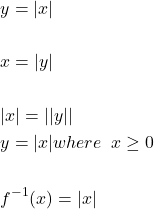
We must observe two things,
- The absolute value cannot be a negative number, therefore,
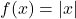 where
where 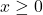 .
. - The function
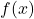 and its inverse does not reflect over
and its inverse does not reflect over 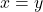 , but
, but 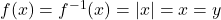 .
.