Equations of Circle - Notesformsc

Table of Contents

In this article, you will learn about distance formula , midpoint , and equations of circle. The circle is a geometric shape that has a special significance in mathematics. To study the circle, in algebraic form, we need to define it in terms of coordinates in a 2d coordinate system also known as Cartesian coordinate system.

Coordinate System

You are familiar with the 2d coordinate system already from previous articles. The 2d coordinate system define an point in terms of an ordered pair $(x, y)$ from origin $(0, 0)$ . The $x$ represents horizontal distance from 0 and $y$ represents vertical distance from $0$ .

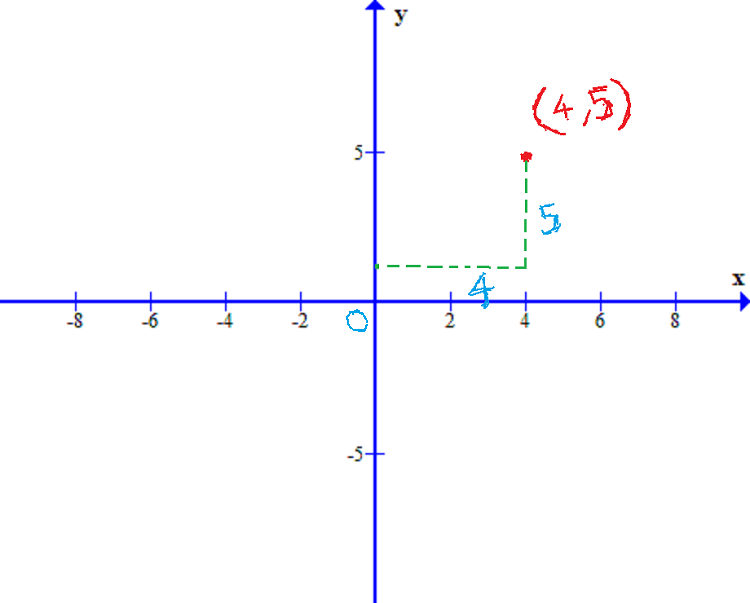
In the figure 1 above, the point $(4, 5)$ is $4$ units in horizontal direction from $0$ and $5$ units in vertical direction from $0$ . Therefore, we must study the circle as a set of points in this 2d coordinate system.

Distance Formula

The distance formula is derived from Pythagorean theorem to find the distance between two points in the coordinate system. Suppose that $P(x_1, y_1)$ and $Q(x_2, y_2)$ are two points in the $xy$ plane.

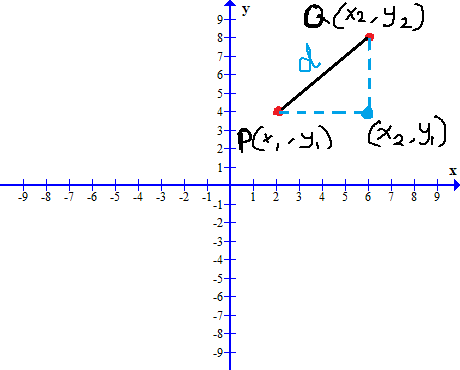
The distance between point $P(x_1, y_1)$ to point $Q(x_2, y_2)$ involve change of $x$ value from $x_1$ to $x_2$ value and change in $y$ value from $y_1$ to $y_2$ . This forms a right triangle in the $xy$ plane.

The distance $d$ is hypotenuse of this right triangle and $(x_1 - x_2)$ and $(y_1 - y_2)$ are the lengths of sides of this right triangle. Therefore, by Pythagorean theorem,

\begin{aligned} &d^2 = (x_1 - x_2)^2 + (y_1 - y_2)^2\\ \\ &Take \hspace{2mm} square \hspace{2mm} root \hspace{2mm} of \hspace{2mm} both\hspace{2mm} sides. \\ \\ &\sqrt{d^2}= \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \\ \\ &d =\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \end{aligned}

The distance formula is $d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$ .

Note that the length $(x_1 - x_2)$ or $(x_2 - x_1)$ does not matter as long as we take $|x_1 - x_2|$ or $|x_2 - x_1|$ . Similarly, we must take positive $y$ value, which is $|y_1 - y_2|$ or $|y_2 - y_1|$ .

Example #1

Find the distance between point $(-4, 7)$ and $(1, 2)$ .

Solution:

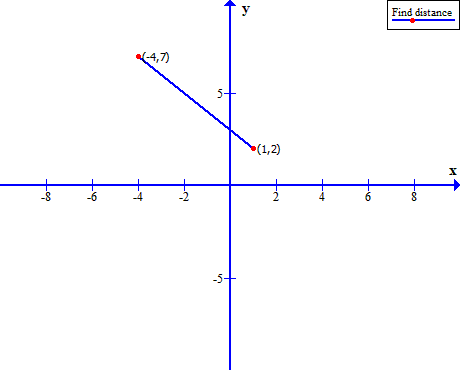
Figure 3 - Find distance between (-4, 7) and (1, 2). — Figure 3 – Find distance between (-4, 7) and (1, 2).

Solution:

\begin{aligned} &Let \hspace{1mm} x_1 = -4 \hspace{1mm} and \hspace{1mm} y_1 = 7,\hspace{1mm}\\ &also \hspace{1mm}x_2 = 1 \hspace{1mm}and\hspace{1mm} y_2 = 2. \hspace{1mm}Then, \\ &(-4) - 1| = |-5| = 5 \hspace{1mm} and \hspace{1mm} |7-2| = |5| = 5 \end{aligned}

The distance between $(-4, 7)$ and $(1, 2)$ is:

\begin{aligned} &d = \sqrt{5^2 + 5^2}\\ \\ &d = \sqrt{50}\\ \\ &d = \sqrt{25 \cdot 2}\\ \\ &d = \sqrt{25} \cdot \sqrt{2} \hspace{1cm} By Rule \sqrt{ab} = \sqrt{a} \cdot \sqrt{b}, {a,b} > 0\\ \\ &d = 5\sqrt{2} \end{aligned}

Mid-Point Formula

Given any two point on the $xy$ plane, you can find the mid-point $M(x, y)$ . If $P(x_1, y_1)$ and $Q(x_2,y_2)$ are two points on the $xy$ plane.

Then the mid-point formula is given as

\begin{aligned} M(x, y) = \left( \frac{x_1 + x_2}{2},\frac{y_1 + y_2}{2}\right ) \end{aligned}

Example #2

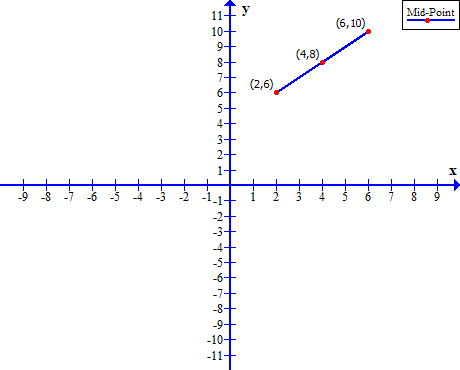
Find the mid-point $M(x, y)$ of points $(2, 6)$ and $(6,10)$ .

Solution:

We can easily find the mid-point $M(x, y)$ using the mid-point formula, which is $\left( \frac{x_1 + x_2}{2},\frac{y_1 + y_2}{2}\right )$ . Given points – $(2, 6)$ and $(6, 10)$ .

\begin{aligned} &Let \hspace{2mm} x_1 = 2, \hspace{2mm} and \hspace{2mm} x_2 = 6\\ \\ &Similarly, \\ \\ &y_1 = 6,\hspace{2mm} and \hspace{2mm} y_2 = 10\\ \\ &Using \hspace{2mm} mid-point \hspace{2mm} formula, \hspace{2mm} get \\ \\ &M(x, y) = \frac{2 + 6}{2}, \frac{6 + 10}{2}\\ \\ &=\frac{8}{2},\frac{16}{2}\\ \\ &=(4,8) \end{aligned}

Therefore, the mid-point $M(x,y) = (4, 8)$ .

Figure 4 - Mid point of (2, 6) and (6, 10) is the point (4, 8). — Figure 4 – Mid point of (2, 6) and (6, 10) is the point (4, 8).

Standard Equation of Circle

A circle on the $xy$ plane is set of all points that equidistant from a fixed point called the center of the circle. The equal distance between center and any point on the circle is called a radius.

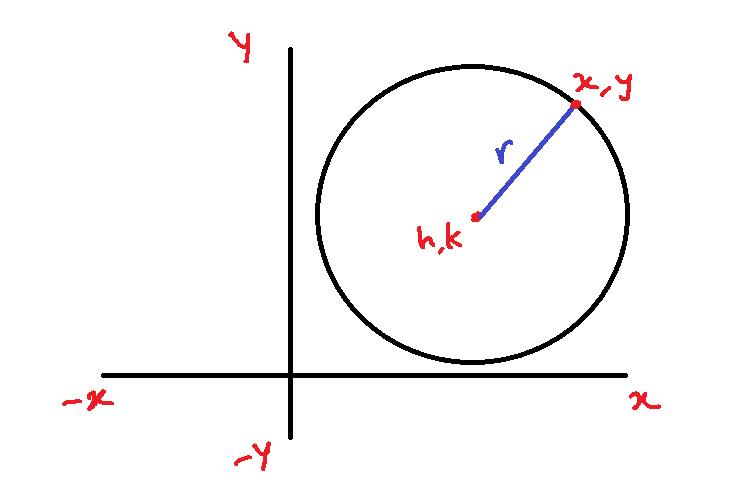
Figure 5 - Circle with radius r and center at (h,k). — Figure 5 – Circle with radius r and center at (h,k).

Consider the circle in figure 5, with radius $r$ and center at $(h, k)$ . The point $(x, y)$ lies on the circle. Therefore, by distance formula, we know that,

\begin{aligned} &r = \sqrt{(x-h)^2 + (y - k)^2}\\ \end{aligned}

This is the standard equation of a circle with center at $(h, k)$ .

Circle With Center At The Origin

In the co-ordinate system, the origin is point $(0, 0)$ . A circle whose center is at $(h, k) = (0, 0)$ has the following equation.

\begin{aligned} &r = \sqrt{(x - 0)^2 + (y - 0)^2}\\ \\ &r = \sqrt{x^2 + y^2}\\ \\ &or\\ \\ &r^2 = x^2 + y^2 \end{aligned}

Example #3

Find the radius of a circle whose center is at $(1, 2)$ and the point $(7, 10)$ lies on the circle.

Solution:

Given center $(h,k) = (1,2)$ and a point $(x, y) = (7, 10)$ , we can use the standard equation of the circle to find the length of radius $r$ .

\begin{aligned} &r = \sqrt{(x-h)^2 + (y - k)^2}\\ \\ &r = \sqrt{(7-1)^2 + (10-2)^2} \\ \\ &r = \sqrt{6^2 + 8^2}\\ \\ &r = \sqrt{36 + 64}\\ \\ &r = \sqrt{100} \\ \\ &r = 10 \hspace{2mm} \end{aligned}

Therefore, the length of radius is $10$ for circle whose center is at $(1, 2)$ and $(7, 10)$ is a point on the circle.

Example #4

Find the center $(h, k)$ of the circle whose radius $5$ and the point $(6,8)$ . Also, $k = h + 1$ .

Solution:

We are given the value of radius $r = 5$ and the point $(6, 8)$ on the circle. To find the center point $(h, k)$ of the circle, we must use the distance formula which is $r = \sqrt{(x-h)^2 + (y - k)^2}$ and the value of $k = h + 1$

\begin{aligned} &r = \sqrt{(x-h)^2 + (y-k)^2}\\ \\ &5= \sqrt{(6 - h)^2 + (8-k)^2}\\ \\ &But, \hspace{2mm} k = h + 1 \\ \\ &5= \sqrt{(6 - h)^2 + (8-(h+1))^2}\\ \\ &5 = \sqrt{(6 - h)^2+ (7 - h)^2)}\\ \\ &5 = \sqrt{36 - 12h + h^2 + 49 - 14h + h^2}\\ \\ &5 = \sqrt{85 - 26h + 2h^2 }\\ \\ &Square \hspace{2mm} both\hspace{2mm} sides \\ \\ &25 = 85 - 26h + 2h^2 \\ \\ &2h^2 - 26h + 85 - 25 = 0\\ \\ &2h^2 - 26h + 60 = 0\\ \\ &h^2 - 13h + 30 = 0 \\ \\ &(h - 3) (h - 10) = 0\\ \\ &By \hspace{2mm} zero\hspace{2mm} product \hspace{2mm} property\\ \\ &\therefore x = 3 \hspace{2mm} or \hspace{2mm} x = 10 \end{aligned}

We try to use the value of $x$ in the equation. It seems that $x = 3$ seems more appropriate. Let us verify.

\begin{aligned} &5 = \sqrt{(6-3)^2+(8-4)^2}\\ \\ &5 = \sqrt{3^2 +4^2 } \hspace{1cm} \because k = h + 1 = 3 + 1 = 4\\ \\ &5 = \sqrt{9 + 16}\\ \\ &5 = \sqrt{25 }\\ \\ &\therefore 5 = 5 \end{aligned}

General Equation Of Circle

Suppose a circle has center at $(3, 7)$ with a point on the circle $(x, y)$ . Therefore, we can find the standard equation of the circle using,

\begin{aligned} &r^2 = (x - h)^2 + (y - k)^2\\ \\ &r^2 = (x - 3)^2 + (y - 7)^2\\ \\ &r^2 = x^2 - 6x + 9 + y^2 - 14y + 49\\ \\ &r^2 = x^2 + y^2 - 6x - 14y + 58 \end{aligned}

Therefore, the general equation of circle is $x^2 + y^2 + Ax + By + C = r^2$ where $A, B, C$ are real constants.

Example #5

Given the general equation of circle $r^2 = x^2 + y^2 -6x -14y + 58$ find the coordinates for center $(h, k)$ of the circle.

Solution:

Given general equation of circle. We will solve it step-by-step. First group the similar variables together and move constant to the right side of the equation.

\begin{aligned}x^2 - 6x + y^2 -14y = - 58\end{aligned}

Now solve for $x$ and $y$ by completing the square. Note that you have to add same value on both side of the equation.

[\begin{aligned}(x^2 - 6x + 9 ) + (y^2 - 14y + 49) = - 58 + 9 + 49\end{aligned}

The equation is in standard form and we can find the value of $(h, k)$ easily.

[\begin{aligned}(x - 3)^2 + (y - 7)^2 = 0^2\end{aligned}

The center of the circle is at $(h, k) = (3, 7)$ .