In this article, we you will learn about composite functions, it means that a function can become input of another function. Before you learn about the composite functions, you must be familiar with the arithmetic of functions which means given two function , you will be able to perform basic arithmetic operations on the function itself. Identifying Domain
Sometimes the function expression is given, but domain is not specified. In such cases, you must identify the domain of given function. Suppose
![]()
![]()
Why this is important ? because when we perform arithmetic operations on two or more functions the domain of new function is set of all real numbers that belong to both ![]() and
and ![]() , that is,
, that is, ![]() .
.
Arithmetic Operations on Functions
Normal arithmetic operations are possible on functions too. If ![]() and
and ![]() are two functions, then there are four operations possible on these functions.
are two functions, then there are four operations possible on these functions.
- Sum
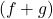
- Difference
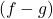
- Product
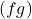
- Quotient
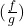
Now we discuss about each of these operations.
Sum of functions
The sum of functions is
![]()
The expressions of both functions are added together to form a new function. For example, if ![]() and
and ![]() , then
, then
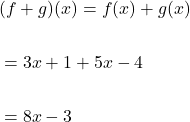
Difference of functions
The difference of functions is
![]()
The expressions of function ![]() is subtracted from expression of function
is subtracted from expression of function ![]() to form a new expression for
to form a new expression for ![]() . For example, if
. For example, if ![]() and
and ![]() , then
, then
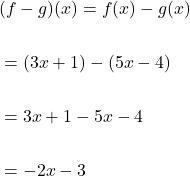
Product of functions
The product of the functions is
![]()
The expressions of function ![]() and
and ![]() is multiplied to get the new product expression of
is multiplied to get the new product expression of ![]() . Each term is of
. Each term is of ![]() is multiplied with each term of
is multiplied with each term of ![]() . For example, if
. For example, if ![]() and
and ![]() are two expressions, then
are two expressions, then
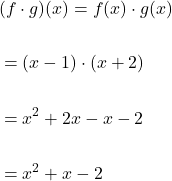
Quotient of functions
The quotient of functions is obtained by dividing two functions, which is
![]()
The functions are divided to get the quotient, however, there is one condition, that is, ![]() , otherwise the quotient of function will be “divide by 0” which is “undefined“.
, otherwise the quotient of function will be “divide by 0” which is “undefined“.
Therefore, if ![]() and
and ![]() , then
, then
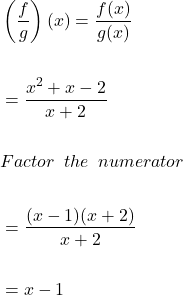
The domain of ![]() ,
, ![]() ,
,![]() is set of all reals numbers that are common to domain of
is set of all reals numbers that are common to domain of ![]() and
and ![]() which is
which is ![]() except where
except where ![]() for
for ![]() .
.
Composite Functions
The composite functions or the idea of composition of functions is simple. Suppose there are two functions, ![]() and
and ![]() , then if function
, then if function ![]() becomes input for function
becomes input for function ![]() , it is called “composition of function
, it is called “composition of function ![]() with function
with function ![]() or simply a composite function.
or simply a composite function.
Let us try to understand this with an example, suppose Nancy work as a maid, and get paid ![]() amount every week and after paying taxes she receives only
amount every week and after paying taxes she receives only ![]() of her earnings. Each week she spends
of her earnings. Each week she spends ![]() for grocery from her earning . The total earning of Nancy after paying taxes can be defined by function
for grocery from her earning . The total earning of Nancy after paying taxes can be defined by function ![]() . Her savings after expense of
. Her savings after expense of ![]() can be defined as function
can be defined as function ![]() .
.
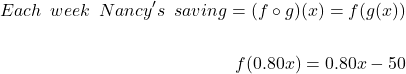
If her gross earning is ![]() , then her saving would be
, then her saving would be
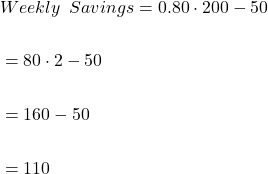
Therefore, total saving after paying taxes and expenses of ![]() is
is ![]() .
.
What is the domain of a composite function?
If ![]() is a composite function such that
is a composite function such that ![]() . Then the domain of composite function must be
. Then the domain of composite function must be
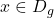 meaning “
meaning “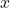 must be in the domain of
must be in the domain of 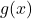 .
.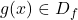 meaning “
meaning “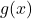 must be in the domain of
must be in the domain of 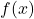 .
.
Therefore, while finding the domain of a composite function, we must first exclude all values of ![]() than can make the function
than can make the function ![]() “invalid”. Also, if
“invalid”. Also, if ![]() happens to be valid, that is,
happens to be valid, that is, ![]() , then
, then ![]() must be valid value for the function
must be valid value for the function ![]() . If
. If ![]() happens to invalid value, then both
happens to invalid value, then both ![]() and
and ![]() must be excluded from the domain of composite function
must be excluded from the domain of composite function ![]() .
.
Decomposing Functions
Like composing two functions, it is possible to decompose a function because we know that “composition of two functions” creates a new function. Consider the following example,
![]()
Here we can clearly see that there are two functions involved in the expression. Therefore, ![]() where
where ![]() which implies that
which implies that ![]() .
.
We can write the function ![]() and
and ![]() as composition of function
as composition of function ![]() where
where ![]() and
and ![]() .
.
