Complex Numbers - Notesformsc

Table of Contents

Complex numbers are extended number system. The motivation behind complex number is that there is no solution to negative roots. Consider the equation $x^2 = -1$ , there is no $x$ that can satisfy this equation.

Powers Of Imaginary Number i

Therefore, the imaginary number $i$ is introduced as the solution to $x^2 +1 = 0$ .

\begin{aligned} The \hspace{1mm}imaginary \hspace{1mm} number \hspace{1mm} i = \sqrt{-1}, where \hspace{1mm} i^2 = -1 \end{aligned}

Now, it is possible to find square root of any negative number.

Example #1

Find the square root of $-64$ .

Solution:

The square root of a negative number is possible using complex number .

\begin{aligned} &\sqrt{-64} = \sqrt{(-1) \cdot 64}\\ \\ &= \sqrt{-1} \cdot \sqrt{64}\\ \\ &= i \cdot 8\\ \\ &\therefore \sqrt{-64} = 8i \end{aligned}

There are few things to note here, firstly, the product property of square roots does not apply for negative numbers, meaning $\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}$ only works when ${a,b} \geq 0$ . Since, we are able to use an imaginary number, it is fine to use the product property of square roots.

Secondly, you must write imaginary number $i$ to the left of any radical. For example, $i\sqrt{6}$ is the right way, and $\sqrt{7}i$ will create confusion. You can write imaginary number $i$ to the right of a real number. For example, $6i$ .

What is a complex number ?

Complex number is extended number system. In a complex number , there are two parts – real part and imaginary part. Therefore, real numbers are subset of complex numbers as shown in the following figure.

A standard form of complex number is $a + bi$ where $a$ is real number and $bi$ is imaginary part of the complex number.

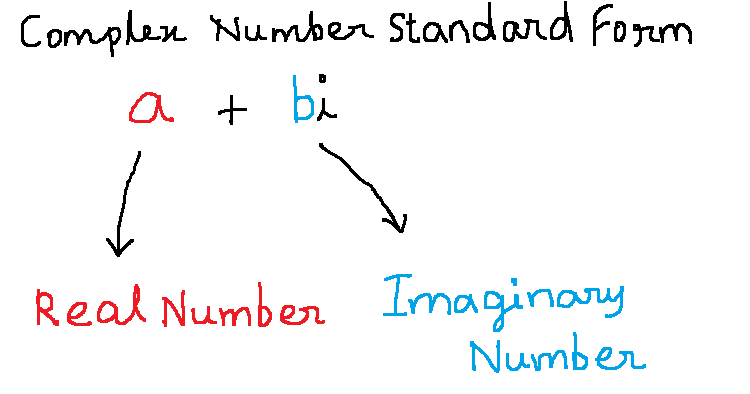
Figure 2 - The standard form of complex number has two parts - real and imaginary — Figure 2 – The standard form of complex number has two parts – real and imaginary

Real Part Of Complex Numbers

Any real number is a complex number of the form $a + bi$ where $b = 0$ . We can rewrite this complex number as $a + 0i$ .

Imaginary Part Of Complex Numbers

The imaginary part is called pure imaginary number when the real number $a = 0$ , therefore, we can write the pure imaginary numbers as $0 + bi$ .

Equality Of Complex Numbers

Complex numbers are equal if their real part and imaginary part are equal. Suppose $a + bi$ and $c + di$ are two complex numbers, then

\begin{aligned} &a + bi = c + di\\ \\ &If \hspace{2mm} and\hspace{2mm} only \hspace{2mm} if \\ \\ &a = c \hspace{2mm} and\hspace{2mm} b = d\\ \end{aligned}

Adding And Subtracting Two Complex Numbers

To add complex number is simple because you need to add the real parts and imaginary parts of two or more complex numbers separately. If $a + bi$ and $c + di$ are two complex numbers, then their addition is

\begin{aligned} &(a + bi) + (c + di) = (a + c) + (b + d)(i)\\ \end{aligned}

Similarly, subtracting two or more complex number requires us to subtract the real parts and the imaginary parts separately. If $a + bi$ and $c + di$ are two complex numbers in standard form, their subtraction is

\begin{aligned} &(a + bi) - (c + di) = a + bi - c - di\\ \\ &=(a -c) + (b - d)(i) \end{aligned}

We will look at some examples to understand this better.

Example #2

Add the following complex numbers and write results in standard form: $(3 + 5i) + (7 + 2i)$ .

Solution:

\begin{aligned} &(3 + 5i) + (7 + 2i)\\ \\ &=(3 + 7) + (5 + 2)(i)\\ \\ &=10 + 7i \end{aligned}

Example #3

Subtract the following complex numbers and write results in standard form: $(5 + i) - (6 + 3i)$ .

Solution:

\begin{aligned} &(5 + i) - (6 + 3i)\\ \\ &(5 - 6) + (1 - 3)(i)\\ \\ &-1 + (-2)(i)\\ \\ &-1 -2(i) \end{aligned}

Multiplying Complex Numbers

Multiplying two complex number is similar to multiplying any algebraic expression except that you have to remember the powers of “iota”. Suppose $a + bi$ and $c + di$ are two complex numbers then their multiplication is

\begin{aligned} &(a + bi)(c + di) = ac + adi + bci + bd(i \cdot i)\\ \\ &= ac + (ad + bc)i - bd\\ \\ &=ac - bd + (ad + bc)i \end{aligned}

The real terms and the imaginary terms are multiplied separately. This results in square of “iota” in one of the terms which is $-1$ .

Therefore, multiplication of two complex number results in another complex number.

Complex Conjugate

The complex conjugate of complex number $a + bi$ is $a - bi$ , similarly, complex conjugate of $a - bi$ is $a + bi$ .

Remember the difference of square in algebra, where $(a + b)(a - b) = a^2 - b^2$ , similarly, multiplying complex conjugates will result in real numbers.

\begin{aligned} &(a + bi)(a - bi) = a^2 -abi + abi - b^2(i^2)\\ \\ &=a^2 - b^2(-1)\\ \\ &=a^2 + b^2\\ \\ &Similarly,\\ \\ &(a -bi)(a + bi) = a^2 + b^2 \end{aligned}

Clearly, multiplication of complex conjugates results in a real number $a^2 + b^2$ .

Example #6

Find the complex conjugate and product of the complex conjugates of $3 - 2i$ .

Solution:

\begin{aligned} &The \hspace{5px}complex \hspace{5px}conjugate \hspace{5px}of \hspace{5px}3 - 2i \hspace{5px}is \hspace{5px}3 + 2i\\ \\ &The\hspace{5px} product \hspace{5px}of \hspace{5px}complex \hspace{5px}conjugates:\\ \\ &(3 - 2i)(3 + 2i) = 9 - 4 (-1) \hspace{1 cm}\because i^2 = -1\\ \\ &=9 + 4 \\ \\ &=13\\ \\ \end{aligned}

The complex conjugates are very important because it help use to solve division involving complex numbers.

Division of Complex Numbers

Imagine that you are dividing two complex numbers, then the goal of the division should be to obtain a real number in the denominator because we are trying to simplify the expression.

If two complex number, $a + bi$ and $c + di$ are given then you must use complex conjugate of denominator to simply the expression.

\begin{aligned} &\frac{a + bi}{c + di} = \frac{a + bi}{c + di} \cdot \frac{c - di}{c - di}\\ \\ &=\frac{ac -adi + bci + bd}{c^2 + d^2} \\ \\ &=\frac{ac - (ad - bc)i + bd}{c^2 + d^2} \end{aligned}

You can see from the above example, that by multiplying with complex conjugate of denominator we get a real number in the denominator.

Application Of Complex Number in Solving Quadratic Equations

The quadratic equation is an equation of following form: $ax^2 + bx + c = 0, a \neq 0$ where $a, b, c$ are real constants. The solution of quadratic equation is given by the formula:

\begin{aligned} &x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \end{aligned}

The expression $d = b^2 - 4ac$ is called the determinant of a quadratic equation.

If the determinant is greater than 0, 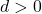$d > 0$ , we have real and distinct roots as solution to quadratic equation.
If the determinant is equal to 0, 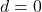$d = 0$ , we have real and equal roots for solution.
If the determinant is less than 0, 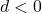$d < 0$ , we have imaginary roots.

When the roots are imaginary , we can solve it using the complex numbers.

Example #7

Solve the following quadratic equation: $x^2 + 2x + 5 = 0$

Solution:

We can use the quadratic formula to solve this quadratic equation.

\begin{aligned} &x = \frac{-2 \pm \sqrt{4 - 20} }{2}\\ \\ &= \frac{-2 \pm \sqrt{-16} }{2}\\ \\ &Therefore, \hspace{2mm}roots \hspace{2mm}are:\\ \\ &\frac{-2 + 4i }{2} \hspace{2mm} ,\frac{-2 - 4i }{2} \end{aligned}

This is just one of the benefit of complex numbers, there are plenty of situations where complex number are helpful in solving, what is otherwise, not possible with only real numbers.

Powers Of Imaginary Number i

What is a complex number ?

Equality Of Complex Numbers

Adding And Subtracting Two Complex Numbers

Multiplying Complex Numbers

Complex Conjugate

Division of Complex Numbers

Application Of Complex Number in Solving Quadratic Equations

Ads Blocker Detected!!!