In the previous article, where we introduce polynomials, a brief introduction to the roots of quadratic equations were discussed with some examples. Now you are going to learn the zeros of polynomial in more detail.
The idea of zero is that to find those x values for which ![]() and it is the x-intercepts in case of quadratic equations which is also a polynomial of degree 2.
and it is the x-intercepts in case of quadratic equations which is also a polynomial of degree 2.
Rational Zero Theorem
As we mentioned earlier, the zeros or roots of a polynomial ![]() is nothing but those values of
is nothing but those values of ![]() for which
for which ![]() .
.
If ![]() is a polynomial with integer coefficients, then
is a polynomial with integer coefficients, then ![]() is the rational zero of the polynomial
is the rational zero of the polynomial ![]() where
where ![]() is the factor of constant term
is the factor of constant term ![]() and
and ![]() is the factor of leading coefficient
is the factor of leading coefficient ![]() .
.
This is could be understood with the help of an example.
Example #1
Find the rational zeros of ![]() .
.
Solution:
The constant term is ![]() and its factors are
and its factors are ![]() .
.
Similarly, the leading coefficient is ![]() whose factors are
whose factors are ![]() .
.
Therefore,
Rational Zeros = ![]()
![]()
There are total 8 roots for this polynomial equation. The actual roots are ![]() .
.
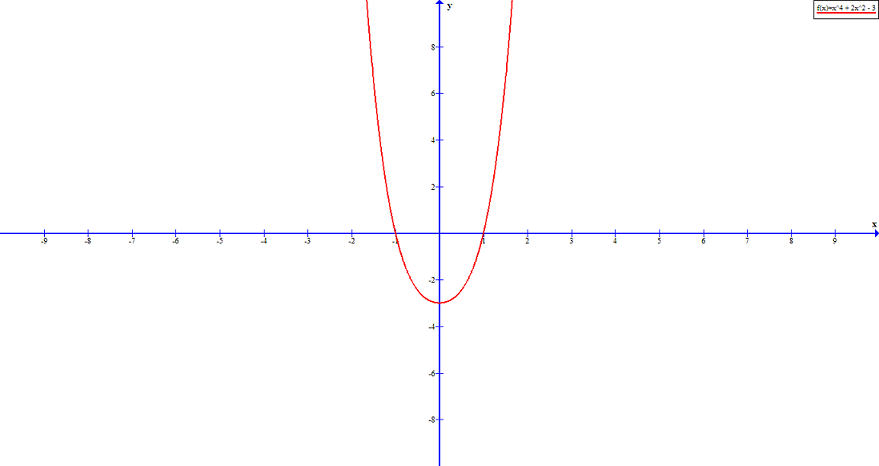
 shows root at -1 and 1
shows root at -1 and 1How To Use The Rational Zero Theorem?
We can use the rational zeros to find the real zero of the polynomial. Note that the polynomial is divided by ![]() such that
such that ![]() .
.
Example #2
Find the real root of the polynomial ![]() from its rational zeros.
from its rational zeros.
Solution:
The constant term is -3 so the factors of constant terms are ![]() .
.
The leading coefficient term is 1 and the factors of leading coefficient are ![]() .
.
Rational \hspace{2 mm} zeros = \frac{\pm1, \pm3}{\pm1}
= \frac{\pm1}{\pm1}, \frac{\pm3}{\pm1}
=\pm1, \pm3Now we test each of the root to find the real root of the polynomial. For this we have to use synthetic division. If you are not familiar with the synthetic division, read the previous article.
3 : 1 -1 3 -3
3 6 27 ( This solution is not suitable because remainder is 24. The remainder should be 0).
1 2 9 24
1 : 1 -1 3 -3
1 0 3 ( The real root of the polynomial is 1 ).
1 0 3 0
After performing a synthetic division we are able to find the real root of the polynomial ![]() . You can also plot the graph of the polynomial and then look for root which is x-intercept.
. You can also plot the graph of the polynomial and then look for root which is x-intercept.
Solving Polynomial Equations
The rational zeros of polynomials are very helpful when the degrees of polynomial equations are higher. Consider the following example.
Example #3
Find the solution to the polynomial equation: ![]() .
.
Solution:
To find solution we must find all the rational roots.
The factors of constant 6 are ![]() and similarly, the factors of leading coefficient is
and similarly, the factors of leading coefficient is ![]() .
.
The rational coefficients are ![]() .
.
Synthetic Division
Now we can do synthetic division to find the solution.
1 : 2 -3 -11 6
2 5 -6 ( 1 is a root of polynomial f(x).
2 5 -6 0Now we can write the equation as ![]() and remainder is 0.
and remainder is 0.
Example #4
Find the rational root of the following polynomial: ![]() .
.
Solution:
The factors of the constant terms are ![]() .
.
The leading coefficient has following factors : ![]() .
.
The rational roots are ![]() .
.
Synthetic division
To find the factors we now have to use the synthetic division. First we are going test ![]()
1: 1 -2 -6 4
1 1 -5 ( This has a remainder of -1. We need to have remainder of 0 in the last cell.)
1 1 -5 -1
2: 1 -2 -6 4
2 0 -12 ( This has a remainder of -8. We need to have remainder of 0 in the last cell.)
1 0 -6 -8
-2: 1 -2 -6 4
-2 8 -4 ( This has a remainder of 0. )
1 -4 2 0Therefore, the root of the equation is ![]() and
and ![]() is a factor.
is a factor.
f(x) = (x + 2)(x^2 - 4x + 2)
We can use the quadratic formula to solve ![]() and find rest of the roots.
and find rest of the roots.
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \\ \\
= \frac{4 \pm 2\sqrt{2}}{2} \\ \\
x = 2 + \sqrt{2} \hspace{2mm} and \hspace{2mm} x = 2 - \sqrt{2}Fundamental Theorem Of Algebra
The fundamental theorem of algebra states that a polynomial ![]() with a degree
with a degree ![]() has
has ![]() roots. To understand this consider the following graph.
roots. To understand this consider the following graph.
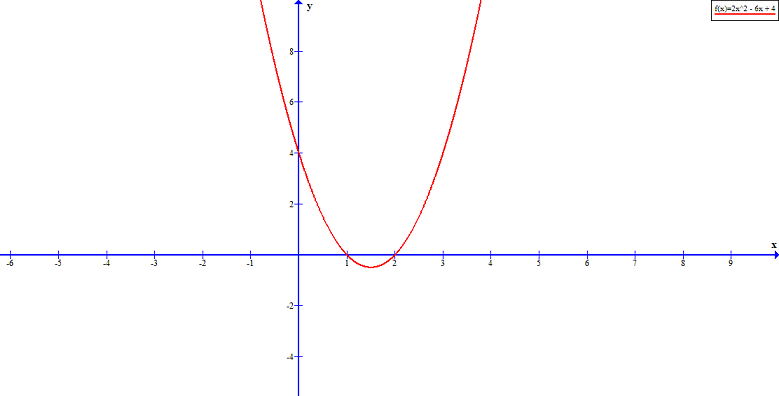
If ![]() is a polynomial with degree
is a polynomial with degree ![]() where
where ![]() , then the equation has one complex root.
, then the equation has one complex root.
Example #5
From our earlier example,
We have ![]() we can factor the second degree polynomial using quadratic formula.
we can factor the second degree polynomial using quadratic formula.
x = \frac{-5 \pm \sqrt{25 - 48}}{4}
= \frac{-5 \pm i\sqrt{23}}{4}
The roots are ![]() and
and ![]() . The complex conjugate is also a root.
. The complex conjugate is also a root.
Linear Factorization
The linear factorization is states that for a polynomial ![]() where
where ![]() , then the polynomial can be written as product of linear factors, called the linear factorization.
, then the polynomial can be written as product of linear factors, called the linear factorization.
![]() where
where ![]() are complex numbers.
are complex numbers.
Example #6
Find the factors of the polynomial: ![]() .
.
Solution:
The factors are ![]()
Using the quadratic formula, ![]()
x = \frac{-6 \pm \sqrt{36-100}}{2}\\ \\
= \frac{-6 \pm \sqrt{-64}}{2}\\ \\
= \frac{-6 \pm i8}{2} \\
Therefore, the roots are ![]()
We can write the polynomial ![]()
This means that roots are rational , irrational and complex or imaginary numbers. In the next section, we discuss a method to find the real roots for polynomial functions.
Rules of Signs
The rules of signs is also called the Descartes’s rules of signs. In a polynomial with degree ![]() , there are at most
, there are at most ![]() real roots, the rule of signs provide specific information about the number of real roots in a polynomial equation.
real roots, the rule of signs provide specific information about the number of real roots in a polynomial equation.
If ![]() is a polynomial with degree
is a polynomial with degree ![]() with real coefficients, then
with real coefficients, then
number of positive real roots are:
- same as the number of sign changes
 in
in  or
or - less than number of sign change
 by a positive even integer.
by a positive even integer. - If there is only one sign change in
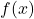 , then there is only one real root.
, then there is only one real root.
number of negative real roots are:
- same as the number of sign changes
 in
in 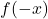 or
or - less than number of sign change
 by a positive even integer.
by a positive even integer. - If there is only one sign change in
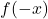 , then there is exactly one real root.
, then there is exactly one real root.
Example #7
Find the number of real roots in the following polynomial:
f(x) = x^3-7x^2+41x-87
Solution:
First we will find the number of sign changes in the given polynomial function.
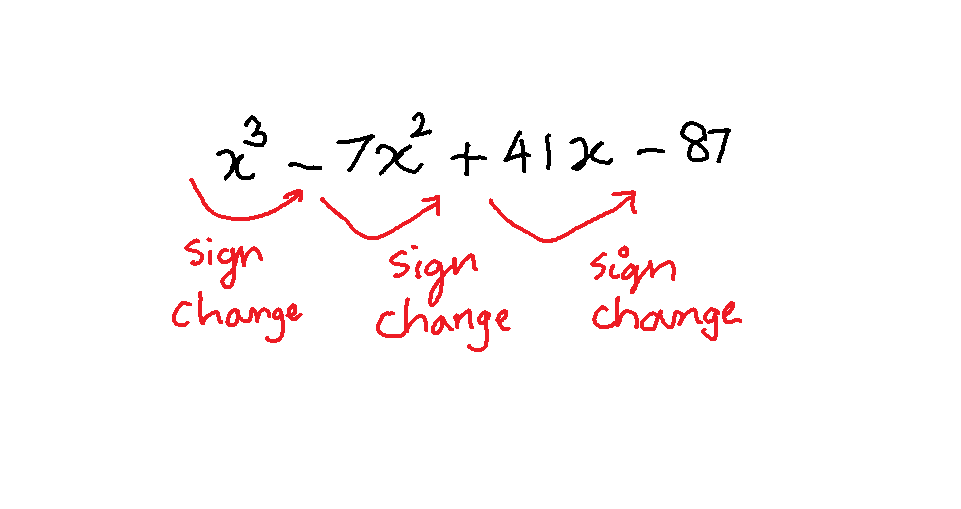
The above equation , there are 3 signs change. Therefore, there are ![]() positive real roots of
positive real roots of ![]() .
.
Or since, ![]() is positive, we have
is positive, we have ![]() positive real root.
positive real root.
We can find the zeros of the polynomial to confirm this. The factors of the polynomials are ![]() .
.
How Rules Of Signs Are Helpful In Solving Polynomials?
The rules of signs helps us to eliminate the unwanted roots from all the rational roots. To illustrate this, we use an example.
Example #8
Find the real roots of the following polynomial: ![]() .
.
Solution:
The number of sign change in this polynomial is 3, therefore, real roots are ![]() or
or ![]() .
.
Let us find the rational roots of this equation.
Factors of the constant terms is ![]() .
.
Factors of the leading coefficient is ![]() .
.
Rational \hspace{2mm}roots = \frac{\pm 1, \pm 2 ,\pm 3, \pm 6}{\pm 1} = \pm 1, \pm 2 ,\pm 3, \pm 6The rules of sign inform us that there is no negative real roots in this equation ![]() . Therefore, we can eliminate all the negative values. The remaining rational roots are
. Therefore, we can eliminate all the negative values. The remaining rational roots are ![]() .
.
Test With Synthetic Division
1: 1 -6 11 -6
1 -5 6 ( Since, the remainder is zero, 1 is a positive real root of 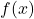 .
1 -5 6 0
3: 1 -6 11 -6
3 -9 6 ( Since, the remainder is zero, 3 is a positive real root of
.
1 -5 6 0
3: 1 -6 11 -6
3 -9 6 ( Since, the remainder is zero, 3 is a positive real root of 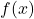 .
1 -3 2 0
2: 1 -6 11 -6
2 -8 6 ( Since, the remainder is zero, 2 is a positive real root of
.
1 -3 2 0
2: 1 -6 11 -6
2 -8 6 ( Since, the remainder is zero, 2 is a positive real root of 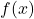 .
1 -4 3 0
There are three real roots as per rules of signs.
.
1 -4 3 0
There are three real roots as per rules of signs.Summary
In this article, you have learned how to find the rational roots, and under special circumstance such as ![]() , there are complex or imaginary roots, so we can find these roots with the linear factorization and rules of signs technique.
, there are complex or imaginary roots, so we can find these roots with the linear factorization and rules of signs technique.
