Engineering Mathematics - Linear Equations of Two Variables

Linear equations form the basis for linear algebra. In the previous lesson, you learned about graph of equations plotted using points on a Cartesian plane, intercepts and symmetry of graphs.

You will learn about a graph of linear equations of two variables in this lesson.

The graph of linear equation is a straight line

\begin{aligned} &y = mx + b \\ \\ &where \\ \\ &m = slope \hspace{2px}of \hspace{2px} the \hspace{2px} line \hspace{2px} and \\ \\ &b = (0, b) = y-intercept \hspace{2px} of \hspace{2px} the \hspace{2px}line \end{aligned}

In the linear equation, the slope is very important and tells lot about the graph. There are 4 slope condition of the line as follows

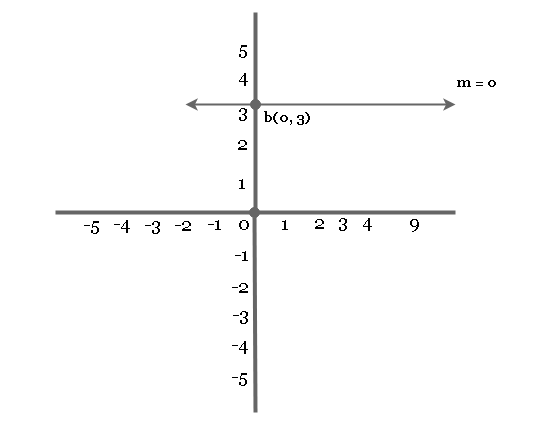
#1 Slope is Zero

Slope is $( m = 0)$ . The value of $m$ is $0$ , hence the line has no slope and it is a straight line.

Consider the equation $y = mx + 3$ , when $m = 0$ . The equation becomes $y = 3$ .

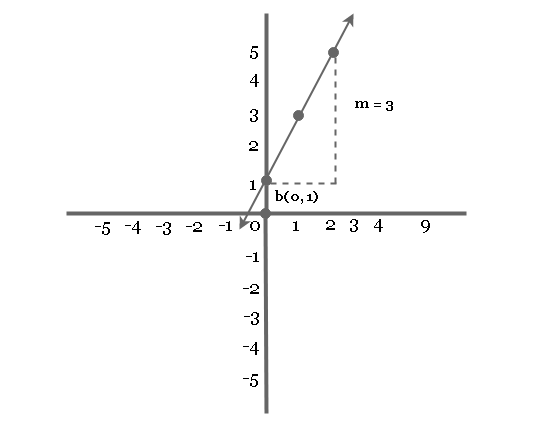
Slope is greater than 0 (m > 0)

When the slope is greater than 0, then it is rising upwards. Consider the following example

y = 2x + 1

where the slope is a positive value with b = 1 as intercept value.

The graph of this equation is given below.

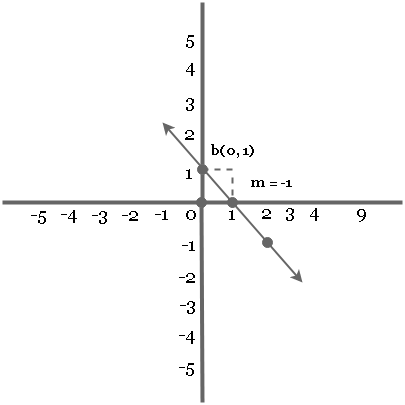
Slope is less than 0 (m < 0)

When the value of $m < 0$ , the slope goes downwards. Consider the following example.

y = -1(x) + 1

The value of slope is $-1$ and b intercept is $(0, 1)$ .

Note: then a vertical line has no slope and its slope is undefined.

The above form of equation of a line is called point-slope form.

The Slope of a line passing through Two-Points

Suppose a line is passing through two points $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ . Then the slope of the line $m$ is given by following.

m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}

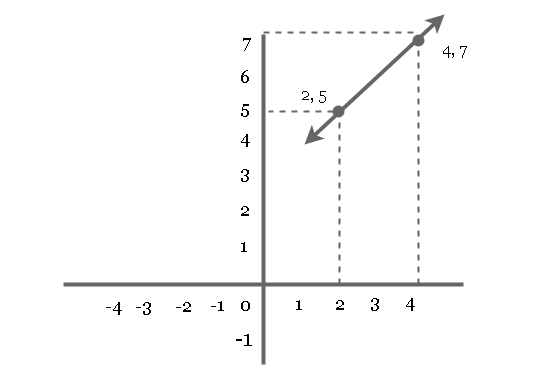
m = \frac{y_{1} - y_{2}}{x_{1} - x_{2}}

For example, Consider 2 points – (2, 5) and (4, 7). Then their slope is given by

\begin{aligned} &m = \frac{7 - 5}{4 - 2}\\\\ &m = \frac{2 }{2}\\\\ &m = 1 \end{aligned}

Therefore, the slope of the line is 1.

Slope of Parallel Lines ( m1 = m2)

The slope of a parallel line is same, because essentially they both are the same line just shifted above or below by few units.

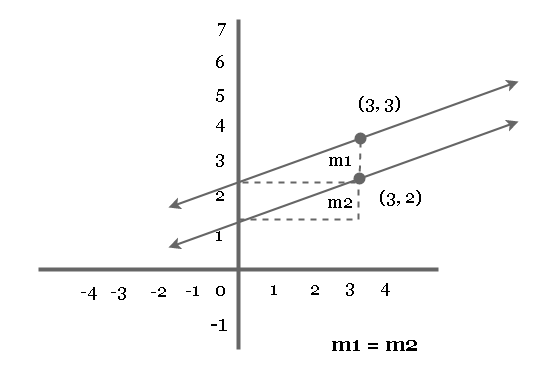
In the diagram above, both lines have the same slope. This could be proved easily using the equations of both lines.

\begin{aligned} &y_1 = m_{1}x + 2       (1)\\ &y_2 = m_{2}x + 1       (2) \end{aligned}

Consider the above example, let $x = 3$ , then the equations become

\begin{aligned} &3 = m_{1}(3) + 2  \hspace{1cm}(1)\\ &3m_1 = 1\\ &2 = m_{2}(3) + 1 \hspace{1cm} (2)\\ &3m_2 = 1 \end{aligned}

Therefore,

$m1 = m2$ for parallel lines.

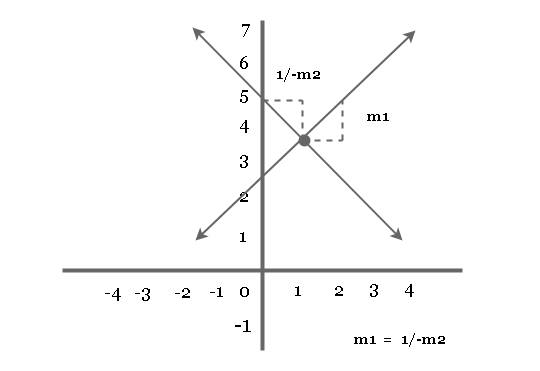
Slope of Perpendicular Lines (m1 = 1/-m2)

The perpendicular line make an angle of $90^\circ$ degrees. The slope of two line that are perpendicular to each other is

m_1 = \frac{1}{-m_2}

The graph of perpendicular lines shows the slopes.