The graph of equation has symmetry along the x-axis or y-axis. In this article, the symmetry of a graph of function is defined in terms of even and odd function.
Prerequisite for this articles is listed below.
Even Function
Let’s understand the even functions first. The function ![]() is even function, if for every x in domain of
is even function, if for every x in domain of ![]() .
.
f(-x) = f(x)
For example,
Let ![]() be a function where
be a function where
f(x) = x^2
The function will square any input value for ![]() and output
and output ![]() . Let us put some values for
. Let us put some values for ![]() , see the following table of values.
, see the following table of values.
| x | y = f(x) | point |
| -2 | 4 | (-2, 4) |
| -1 | 1 | (-1, 1) |
| 0 | 0 | (0, 0) |
| 1 | 1 | (1, 1) |
| 2 | 4 | (2, 4) |
The table shows that any ![]() values is equal to
values is equal to ![]() .
.
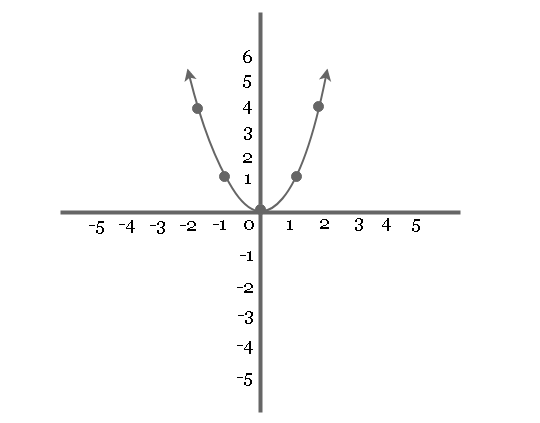
The graph of even function is symmetric along the y-axis.
Odd Functions
The odd function is different from even function in terms of symmetry of graph of the function. The function ![]() is odd function if for every
is odd function if for every ![]() in the domain of
in the domain of ![]() .
.
f(-x) = -f(x)
Consider the following table of points for the function ![]() .
.
| x | y = f(x) = x + 1 | point |
| -3 | -2 | (-3, -2) |
| -2 | -1 | (-2, -1) |
| -1 | 0 | (-1, 0) |
| 0 | 1 | (0, 1) |
| 1 | 2 | (1, 2) |
| 2 | 3 | (2, 3) |
The graph of odd function shows that ![]() is
is ![]() .
.
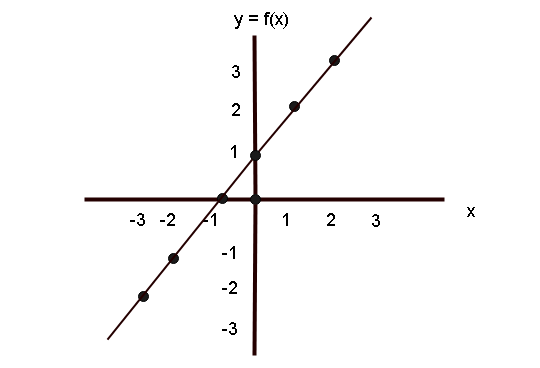
The graph of odd function is symmetric along the y-axis.