Rational functions are special functions that you cannot call polynomials, but are obtained by dividing polynomials. In other words, they are the quotients of the polynomial division.
A rational function is of form ![]() where
where ![]() and
and ![]() are polynomials and
are polynomials and
![]() . The domain of rational function can be any real numbers except those that makes
. The domain of rational function can be any real numbers except those that makes ![]() .
.
Example #1
![]() is a rational function. The function accept all real number except 1. The value 1 makes the function invalid. Hence, we can write domain of the
is a rational function. The function accept all real number except 1. The value 1 makes the function invalid. Hence, we can write domain of the ![]() as
as ![]() .
.
Example #2
Find the domain of rational function ![]() .
.
Solution:
The rational function accepts all values, except ![]() , which we can write in interval notation also,
, which we can write in interval notation also, ![]() .
.
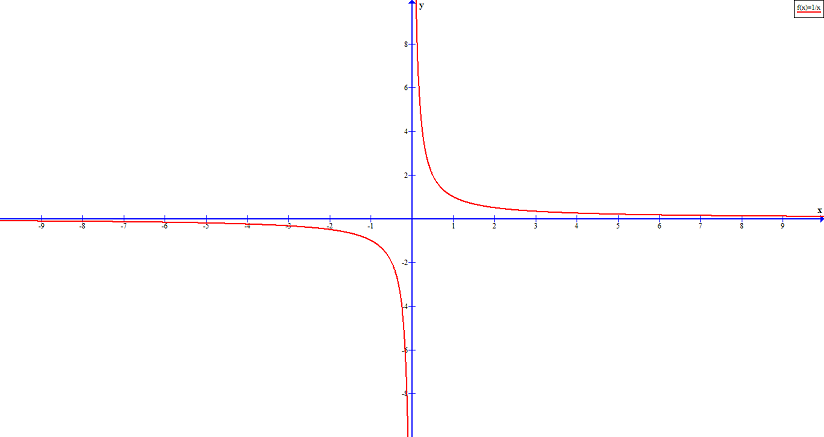
The Reciprocal Function
The simplest of rational function is the reciprocal function ![]() . The function accepts all real values except
. The function accepts all real values except ![]() .
.
Let us plot the graph of this rational function for following values.
| X | -1 | –0.5 | -0.1 | -0.01 | -0.001 | -0.0001 |
| F(x) | -1 | -2 | -10 | -100 | -1000 | -10000 |
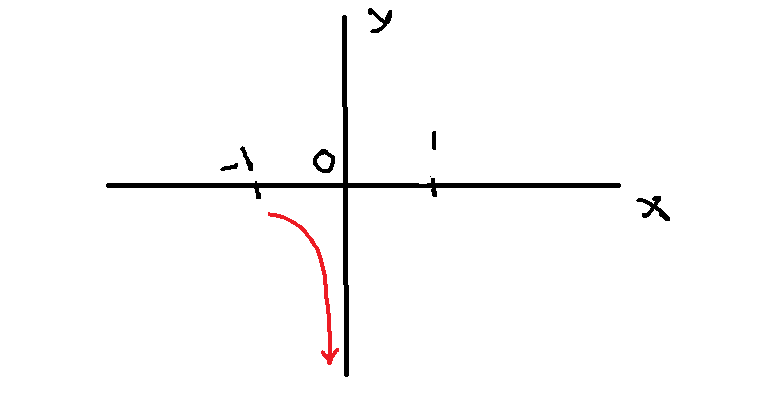
As the ![]() value approaches
value approaches ![]() from left, the value of
from left, the value of ![]() becomes smaller and smaller boundlessly to
becomes smaller and smaller boundlessly to ![]() . This can be shown with the arrow notation as follows.
. This can be shown with the arrow notation as follows.
![]()
![]() ,
, ![]()
What happens when ![]() comes closer to
comes closer to ![]() from right side.
from right side.
| X | 0.0001 | 0.001 | 0.01 | 0.1 | 0.5 | 1 |
| F(x) | 10000 | 1000 | 100 | 10 | 2 | 1 |
![]() ,
,![]() .
.
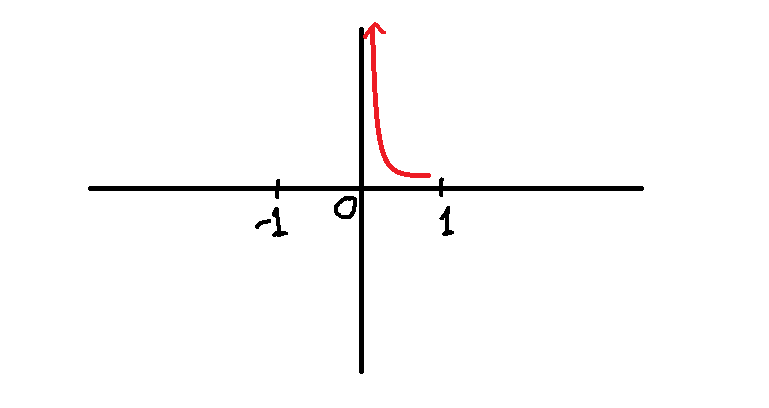
As the ![]() value approaches 0 from right , the value of
value approaches 0 from right , the value of ![]() increases boundlessly to positive
increases boundlessly to positive ![]() . This is shown above with arrow notation.
. This is shown above with arrow notation.
What happens when the value of ![]() moves away from
moves away from ![]() , that is,
, that is, ![]() increases or decreases boundlessly ?
increases or decreases boundlessly ?
| X | 1 | 10 | 100 |
| F(x) | 1 | 0.1 | 0.01 |
| X | -1 | -10 | -100 |
| F(x) | -1 | -0.1 | -0.01 |
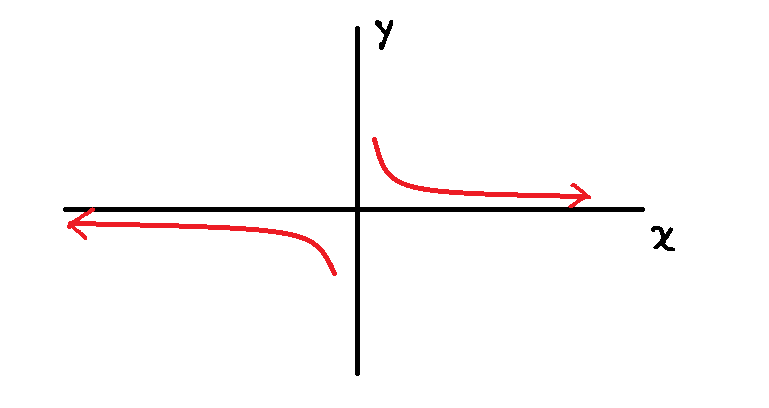
When the ![]() value increases or decreases boundlessly, then the
value increases or decreases boundlessly, then the ![]() approaches
approaches ![]() , but not touching
, but not touching ![]() .
.
This is shown in arrow notation below.
![]() ,
, ![]() and
and ![]() ,
, ![]() .
.
Vertical Asymptotes
There are several rational functions, out of which ![]() is an interesting one. The graph of this function is reflected across the y-axis.
is an interesting one. The graph of this function is reflected across the y-axis.
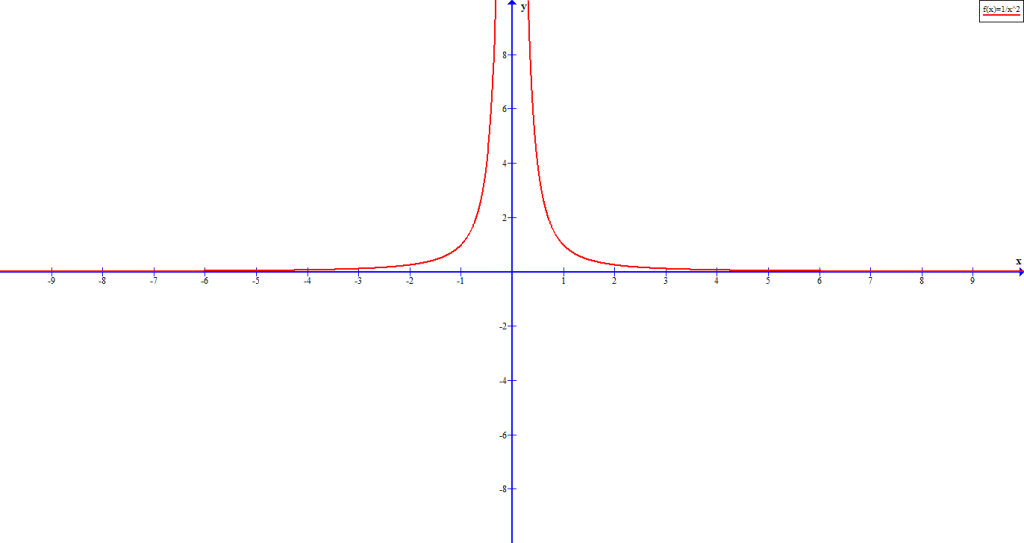
We can describe the end behavior of this graph in the following manner.
| | |
| | |
The line ![]() is called the vertical asymptote of the graph. A rational function can have
is called the vertical asymptote of the graph. A rational function can have
- one vertical asymptote
- many vertical asymptotes
- or no vertical asymptotes
The end behavior of rational function around vertical asymptote are:
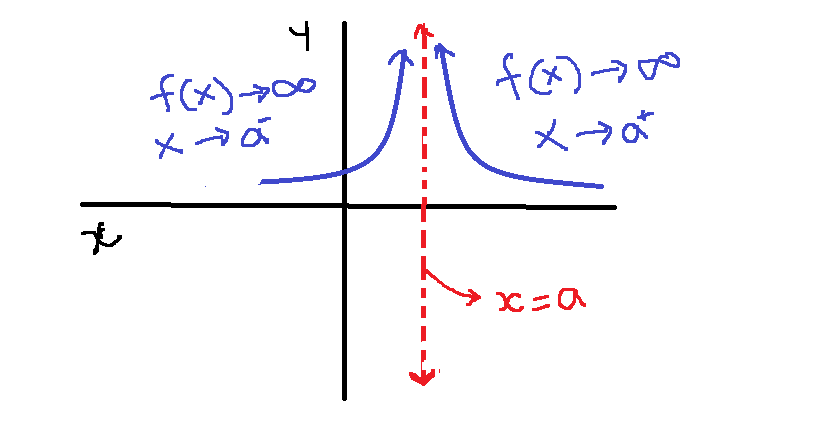
Figure 7 – As x approaches a, f(x) increases boundless
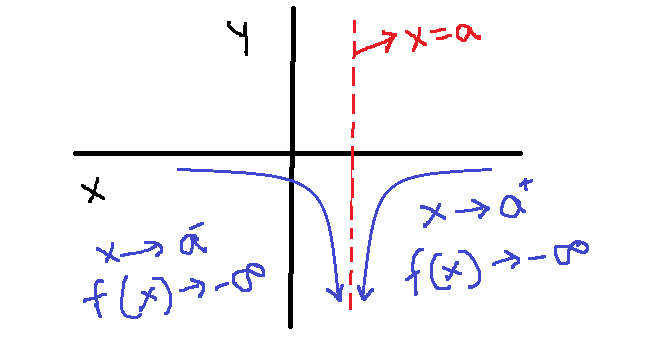
As the value of ![]() approaches the
approaches the ![]() , the
, the ![]() increases or decreases without bound.
increases or decreases without bound.
This increase or decrease in end behavior is useful in study of calculus. We can describe how the value of ![]() and the function changes using limits.
and the function changes using limits.
The ![]() moves closer to
moves closer to ![]() from left or right, the end behavior changes is shown in limits below.
from left or right, the end behavior changes is shown in limits below.
| | |
| | |
How To Locate The Vertical Asymptotes ?
If the rational function have vertical asymptotes, then it can be found easily. We know that ![]() where
where ![]() and
and ![]() are two polynomials. There are two conditions to find the vertical asymptotes:
are two polynomials. There are two conditions to find the vertical asymptotes:
- The polynomials
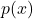 and
and 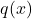 have no common factors, if they have common factor must be eliminated.
have no common factors, if they have common factor must be eliminated. - The value
 must be zero of the polynomial
must be zero of the polynomial 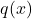 , that is, denominator. If
, that is, denominator. If  is zero then
is zero then  is the vertical asymptotes.
is the vertical asymptotes.
You can understand this with the help of an example.
Example #3
Find the vertical asymptotes of the rational function: ![]()
Solution:
The given equation ![]() does not have any common factors, therefore, meet the first condition. The denominator accepts all real numbers except
does not have any common factors, therefore, meet the first condition. The denominator accepts all real numbers except ![]() which makes it
which makes it ![]() .
.
Therefore, ![]() is the vertical asymptote in the graph of rational function.
is the vertical asymptote in the graph of rational function.
Example #4
Find the vertical asymptote of the rational function: ![]() .
.
Solution:
In the given equation, ![]() has a common factor. We reduce the common factor and the equation becomes
has a common factor. We reduce the common factor and the equation becomes ![]() .
.
The function accepts all real values, ![]() except
except ![]() . Therefore,
. Therefore, ![]() is the vertical asymptotes.
is the vertical asymptotes.
Example #5
Find the vertical asymptotes for the rational function: ![]() .
.
Solution:
The function has no common factor, but there is no ![]() value for which the denominator is
value for which the denominator is ![]() . Therefore, the function does not have a vertical asymptote.
. Therefore, the function does not have a vertical asymptote.
In some cases, the denominator is shows that it has a zero, but after reducing the common factors, the resultant expression has a totally new vertical asymptote.
Example #6
Find the vertical asymptote for the equation: ![]() .
.
Solution:
At first we see that the equation has a zero ![]() , but when the equation is reduced after reducing the common factors, we get
, but when the equation is reduced after reducing the common factors, we get ![]() and the vertical asymptote is
and the vertical asymptote is ![]() .
.
Horizontal Asymptotes
The equation ![]() represents “vertical asymptote“, similarly,
represents “vertical asymptote“, similarly, ![]() represents the “horizontal asymptotes“. There may be several vertical asymptotes, but there is only one horizontal asymptote.
represents the “horizontal asymptotes“. There may be several vertical asymptotes, but there is only one horizontal asymptote.
The function ![]() , as
, as ![]() increases or decreases without bound
increases or decreases without bound ![]() or
or ![]() , the
, the ![]() approaches
approaches ![]() , which is
, which is ![]() . So, we can say that the horizontal asymptote is that which is defined as
. So, we can say that the horizontal asymptote is that which is defined as ![]() .
.
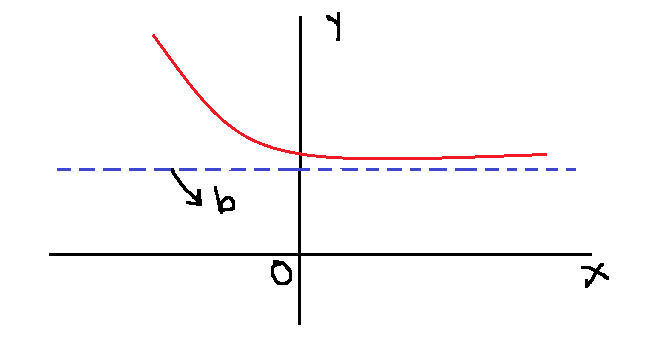
We can write them in limit form as:
| |