Understanding Limits and Continuity

Table of Contents

Limits and continuity of function is where calculus topics starts, however, to know calculus you must complete all lessons of pre- calculus with examples.

Limit of a function is a certain value that a function approaches, whereas a function is said to be continuous when the function has no breaks or drawn without taking the pen away from the paper.

How to understand a limit of a function?

Limit of a function is a certain value on x- axis that a function of x approaches from both the sides. When a function of x approaches to n (where n is an integer), then all the values of x are very close to n from both the side of the number line. For example, when function of x approaches to 2, then the the values near to the limit of a function from the left if 1.9, 1.99, 1.999 etc. and from the right is 2.1, 2.01, 2.001 etc.

Limit with an example

Let us say $f(x) = x^{2} + 2x - 6$ is a function whose limit is 2, then, the limit of a function can be written as $\displaystyle \lim_{x \to 2}$ . This can be showed in the form of a graph.

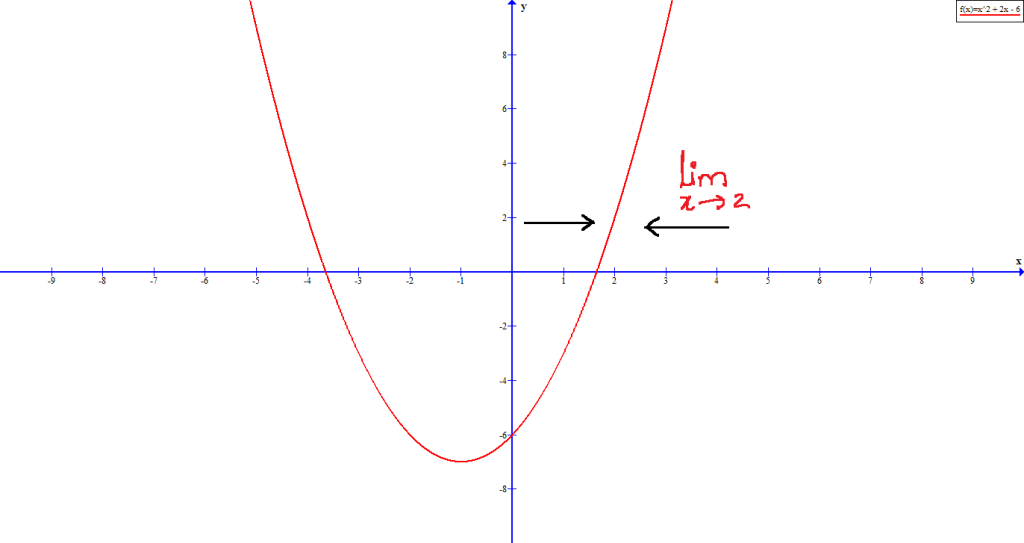
Figure 1 - Limit example, the value of x approaches 2 from left and right side but never equal to 2. — Figure 1 – Limit example, the value of x approaches 2 from left and right side but never equal to 2.

While finding the limit of a function, what should we observe?

Finding the limit of a function is all about observing the particular value a function approaches from left and right. From figure 1, it can be observed that both the right hand limit and left hand limit of a function approaches to the same number. In the above graph, the limit approaches from both right and left to 2.

$\displaystyle \lim_{x \to c^-}$ means that x approaches c from left and reach all numbers smaller than c.
Similarly,
$\displaystyle \lim_{x \to c^-}$ means that x approaches c from right and reach all numbers greater than c.

Note: the value of x is never equal to c.

Continuity of a function

The limits applies to a continuous function. If the function is continuous, then a limit exists, otherwise not.

What is continuity of a given function?

A function is said to be continuous, when graph for the given function shows no breaks or discontinuity at a point or at least in a given interval.

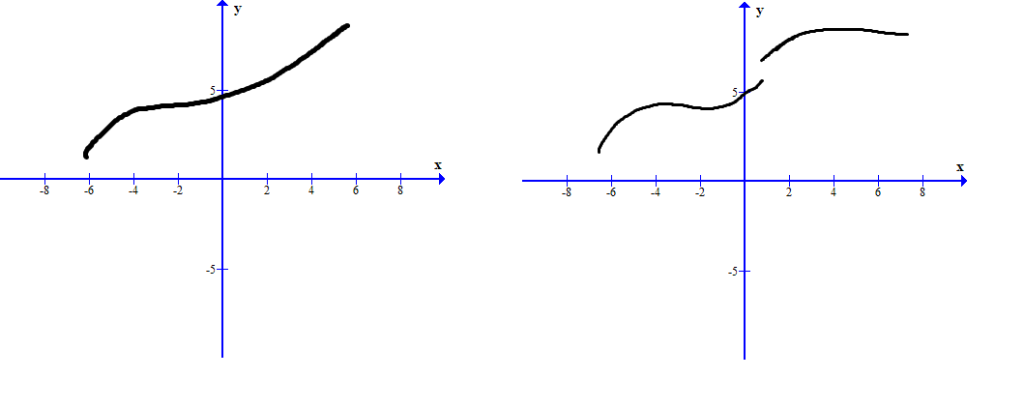
Figure 2 - Continuous and Discontinuous function example — Figure 2 – Continuous and Discontinuous function example

How to find whether a function is continuous?

Continuity of a function can be examined in two ways.

Continuity of a function at a given point
Continuity over a given interval

For finding the continuity of is given function is, the given function should have no breaks at the neighbourhood to a given point.

How to determine the continuity of a function at a given point?

For checking the continuity of a function at a given point, then it must satisfy the following conditions viz.,

The point at which continuity of a function is examined should be within the domain of the function.
Both the left handed and right handed limit of the function approaching to the point should be equal.

Summary

Limit of a function is approached from both the sides.
If the difference between the nearest value and the limit n is $h, h_{1}, h_{2}$ etc., then the values approaching from the left is $n - h, n - h_{1}, n - h_{2}$ .
In the same case, the values approaching from the right is $n + h, n + h_{1}, n + h_{2}$ .
Continuity is defined as a function without any breaks or jumps.