So far you have learnt that square matrix has determinant value and larger the square matrix more difficult it is to compute the determinant through cross multiplication method. The larger matrix is usually broken down into smaller matrix and determinant or minors are calculated. Then assigning signs to these minors will give you cofactors to computer the determinant of the original matrix. Here we will discuss about computing adjoint of square matrix using cofactors.
The Adjugate or Adjoint of a square matrix
The adjugate of a square matrix is also called adjoint matrix which is obtained from matrix of cofactors. To learn about cofactors visit : Cofactors of square matrix.
Suppose ![]() is a square matrix , and
is a square matrix , and ![]() is its cofactor matrix. Then the adjoint of the matrix
is its cofactor matrix. Then the adjoint of the matrix ![]() can be obtained by transposing the cofactor matrix
can be obtained by transposing the cofactor matrix ![]() .
.
Let ![]() be a matrix of size
be a matrix of size ![]() ,and
,and ![]() is the cofactor matrix of
is the cofactor matrix of ![]() . The adjoint of the matrix
. The adjoint of the matrix ![]() is denoted as
is denoted as ![]() .
.
Steps to find Adjoint of a Square Matrix
The steps to find the adjoint of a square matrix is easy as most of the steps you have learned in previous articles already. Here are the steps.
- Check if the given matrix
 is a
is a 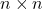 square matrix.
square matrix. - Find the minors of the matrix
 and arrange them in a matrix form according to subscript value.
and arrange them in a matrix form according to subscript value. - Find the cofactors of matrix
 from the given minor matrix and arrange in matrix form according to subscript of each cofactor.
from the given minor matrix and arrange in matrix form according to subscript of each cofactor. - Transpose the cofactor matrix to obtain the adjoint of matrix

Example #1
Find the adjoint of matrix ![]() .
.
A = \begin{bmatrix}2 & 1 & 3\\1 & 5 & 2\\4 & 7 & 3\end{bmatrix}Solution:
We will find solution to this matrix in a step-by-step manner.
Step1: The given matrix ![]() is a
is a ![]() square matrix.
square matrix.
A = \begin{bmatrix}2 & 1 & 3\\1 & 5 & 2\\4 & 7 & 3\end{bmatrix} Step2: We must find the matrix of minors for ![]() .
.
\begin{aligned}
&M_{11} = \begin{vmatrix}5 & 2\\7 & 3\end{vmatrix} = 15-14 = 1\\\\
&M_{12} = \begin{vmatrix}1 & 2\\4 & 3\end{vmatrix} = 3-8 = -5\\\\
&M_{13} = \begin{vmatrix}1 & 5\\4 & 7\end{vmatrix} = 7-20 = -13\\\\
&M_{21} = \begin{vmatrix}1 & 3\\7 & 3\end{vmatrix} = 3-21 = -18\\\\
&M_{22} = \begin{vmatrix}2 & 3\\4 & 3\end{vmatrix} = 6-12 = -6\\\\
&M_{23} = \begin{vmatrix}2 & 1\\4 & 7\end{vmatrix} = 14-4 = 10\\\\
&M_{31} = \begin{vmatrix}1 & 3\\5 & 2\end{vmatrix} = 2-15 = -13\\\\
&M_{32} = \begin{vmatrix}2 & 3\\1 & 2\end{vmatrix} = 4-3 = 1\\\\
&M_{33} = \begin{vmatrix}2 & 1\\1 & 5\end{vmatrix} = 10-1 = 9\\\\
&= \begin{bmatrix}1 & -5 & -13\\-18 & -6 & 10\\-13 & 1 & 9\end{bmatrix}
\end{aligned}Step3: Given the matrix of minors we can quickly find the cofactor matrix by shortcut method. Assign negative or positive sign to minors based on following pattern.
= \begin{bmatrix}+ & - & +\\- & + & -\\+ & - & +\end{bmatrix}Then we get,
\begin{aligned}
&= \begin{bmatrix}(+)1 & (-)-5 & (+)-13\\(-)-18 & (+)-6 & (-)10\\(+)-13 & (-)1 & (+)9\end{bmatrix}\\\\
&\begin{bmatrix}A_{ij}\end{bmatrix} = \begin{bmatrix}1 & 5 & -13\\18 & -6 & -10\\-13 & -1 & 9\end{bmatrix}
\end{aligned} Step4: Finally, transpose the cofactor matrix to get the adjoint of matrix ![]() .
.
\begin{aligned}
&Adj A = \begin{bmatrix}A_{ij}\end{bmatrix}^T = \begin{bmatrix}1 & 5 & -13\\18 & -6 & -10\\-13 & -1 & 9\end{bmatrix}^T\\\\
&Adj A = \begin{bmatrix}1 & 18 & -13\\5 & -6 & -1\\-13 & -10 & 9\end{bmatrix}
\end{aligned}Inverse Matrix Using Adjoint
The adjoint matrix can also be used to find the inverse of a matrix. The only condition is that the determinant must not be zero. If the determinant of a square matrix is nonzero, then the following will give inverse matrix of a matrix ![]() .
.
A^{-1} = \frac{1}{|A|}\times Adj AIn the previous example, we computed the adjoint matrix of A which is
Adj \hspace{3px}A = \begin{bmatrix}1 & 18 & -13\\5 & -6 & -1\\-13 & -10 & 9\end{bmatrix}Let us find the determinant of the matrix by multiplying first row of matrix A and first row of cofactor matrix of A.
\begin{aligned}
&Row \hspace{3px}1 \hspace{3px}of \hspace{3px}A = 2 \hspace{6px}1 \hspace{6px}3 \\\\
&Row \hspace{3px}1\hspace{3px} of\hspace{3px} Cofactor\hspace{3px} of \hspace{3px}A = 1 5 -13
\end{aligned}Therefore,the deterinant of matrix A is,
|A| = 2(1) + 1(5) + 3 (-13) = 2 + 5 -39 = -32
We can compute the inverse of matrix ![]() using determinant and the adjoint matrix.
using determinant and the adjoint matrix.
\begin{aligned}
&A^{-1} = \frac{1}{-32} \times \begin{bmatrix}1 & 18 & -13\\5 & -6 & -1\\-13 & -10 & 9\end{bmatrix}\\\\
&A^{-1} = \begin{bmatrix}-1/32& -9/16&13/32\\ -5/32&3/16&1/32\\13/32&5/16&-9/32\end{bmatrix}
\end{aligned}Readers must check the correctness of the inverse as an exercise.
In the next article, we will discuss about how to find the solution to a system of linear equations using determinant method popularly known as Cramer’s rule.