Some linear systems have no solution; they are called inconsistent systems. If a linear system has at least one solution than it is called consistent system.
To illustrate this with example, consider two linear equations that represents two line on xy-plane given below.
\begin{aligned}
&a_{1}x_{1} + a_{2}x_{2} = b_{1}\\
&a_{3}x_{1} + a_{4}x_{2} = b_{2}
\end{aligned}where either one variable can be zero, not both.
Let us call the lines as ![]() and
and ![]() . A solution to the equation is a point
. A solution to the equation is a point ![]() that satisfy both equations given above.
that satisfy both equations given above.
Possibilities of Solution
There are three possibilities of solution for lines – ![]() and
and ![]() .
.
- No Solutions
- Exactly One Solution
- Infinite Solutions
Let us examine each one of these possibilities closely.
No Solutions
If the lines – ![]() and
and ![]() are parallel, that is, not touching each other, there is no possibility of a common point
are parallel, that is, not touching each other, there is no possibility of a common point ![]() .
.
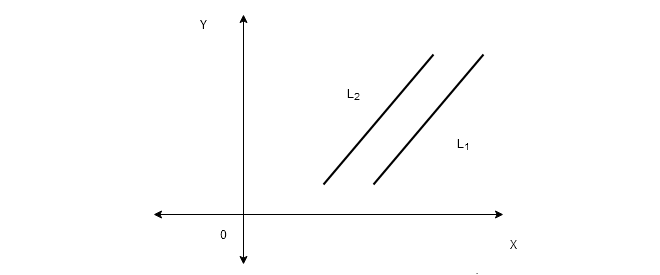
Therefore, the above system has no solution.
Exactly One Solution
Suppose the lines – ![]() and
and ![]() intersect each other exactly at a point
intersect each other exactly at a point ![]() . Then we have exactly one solution to the linear system.
. Then we have exactly one solution to the linear system.
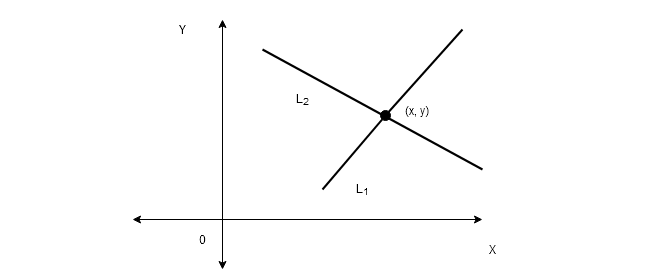
The point ![]() in the above diagram is the only solution that satisfy equation of both the lines.
in the above diagram is the only solution that satisfy equation of both the lines.
Infinite Solutions
When the two lines – ![]() and
and ![]() are the same or overlap each other then we can say that there could be more than one points
are the same or overlap each other then we can say that there could be more than one points ![]() belong to both line.
belong to both line.
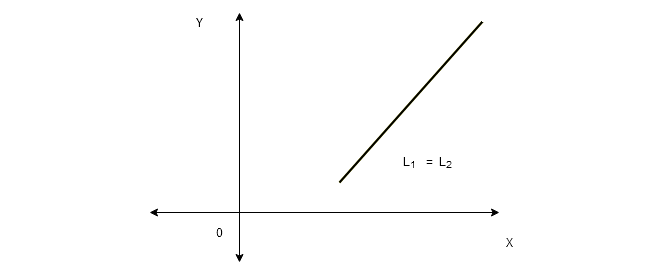
Therefore, the equation has infinite solutions because the line may increase forever in the xy-plane. We can formally say that ” Every linear system has no solution, one solution, or infinitely many solutions“.
Augmented Matrix
We know linear equations and system of linear equations from our earlier discussions. Any system of linear equation with ![]() equations and
equations and ![]() variable
variable ![]() , …,
, …, ![]() is written as
is written as
\begin{aligned}
&a_{11}x_{1} + a_{12}x_{2}+ a_{13}x_{3} = b_{1}\\
&a_{21}x_{1} + a_{22}x_{2}+ a_{23}x_{3} = b_{2}\\
&a_{31}x_{1} + a_{32}x_{2}+ a_{33}x_{3} = b_{3}
\end{aligned}where a’s and b’s are real number constants.
The same equations can be represented using a two-dimensional system called augmented matrix. We usually refer as ‘matrix‘,but the word ‘augmented’ highlights that context of matrix system. We now know from where the matrix came from.
\begin{bmatrix}a_{11} & a_{12} & ... & a_{1n} & b_{1}\\ a_{21} & a_{22} & ... & a_{2n} & b_{2}\\: & : & : & : & :\\a_{m1} & a_{m2} & ... & a_{mn} & b_{m}\end{bmatrix}The double subscript indicate the correct position of a term with respect to rows and columns where rows are equations and columns are terms.
Important points
Here are some important points to consider while constructing a augmented matrix form a system of equations.
- keep the order of a’s according to unknown variables x’s.
- keep the b constant on the right in the same order as in the equation.
Example
Problem #1 : Change the following system of linear equations to augmented matrix.
\begin{aligned}
&3x_{1} + x_{2}+ 6x_{3} = 1\\
&2x_{1} + 2x_{2}+ x_{3} = 7\\
&4x_{1} - 6x_{2}+ 9x_{3} = 5
\end{aligned}Solution : The resultant augmented matrix is
\begin{bmatrix}3 & 1 & 6 & 1\\ 2 & 2 & 1 & 7\\ 4 & -6 & 9 & 5\end{bmatrix}We will consider changing the terms with the help of basic row operations in the next post.
