In the previous article, we have seen how determinant decides whether a system of equation (read square matrix) has inverse, or it has a solution, only when the determinant is not zero. The determinant is obtained from the equation given below.
determinant = \sum \pm a_{1\alpha}a_{2\beta} \cdots a_{nv}To know more about finding determinant in this way , read previous article. Here we will discuss about finding determinant by cross multiplication but before that let us understand the different notations used to represent determinants.
Notation For Determinants
There are several notation for determinants given by earlier mathematicians. Suppose $A$ represents a augmented matrix from a system of linear equations, then determinant of $ A$ is given below.
Let the matrix $A$ be a 2 x 2 matrix.
A = \begin{bmatrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{bmatrix}Different ways to represent determinant of matrix $A$.
\begin{aligned}
&det(A) \hspace{1cm}(1)\\\\
&|A| \hspace{1cm}(2)\\\\
&\begin{vmatrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{vmatrix} \hspace{1cm}(3)
\end{aligned}Determinant as a Function
Imagine determinant to a function that take a square matrix as input and give a single value as output. For example,$f(x) = x^3$ be a function where $x$ could be any real number. Similarly, 
Determinant of $1 \times 1$ Matrix
If $A$ is a matrix with just one element, then its determinant is the same element.
Example #1
Let $A$ be a square matrix of order $1 \times 1$.
A = \begin{bmatrix}2\end{bmatrix}Then the determinant of $A$ is,
|A| = |2| = 2
Determinant of $ 2 \times 2$ Matrix
The determinant of a $2 \times 2$ matrix is obtained by performing cross multiplication. See the following figure.
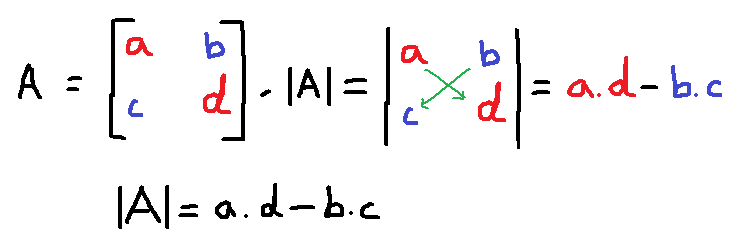
Example #2
Let $A$ be a $2 \times 2$ square matrix. Find the determinant of the matrix $A$.
Solution:
Let the $A$ be 2 x 2 square matrix.
\begin{aligned}
&A = \begin{bmatrix}2 & 3\\1 & 5\end{bmatrix}\\\\
&|A| = a \times d - b \times c\\\\
&|A| = 2 \times 5 - 3 \times 1\\\\
&|A| = 10 - 3 = 7
\end{aligned}Example #3
Let $B$ be a square matrix of order $2 \times 2$. Find the determinant of the matrix $B$.
Solution:
Let $B$ be a square matrix of order $2 \times 2$.
\begin{aligned}
&B = \begin{bmatrix}5 & -1\\4 & -3\end{bmatrix}\\\\
&|B| = a \times d - b \times c\\\\
&|B| = 5 \times (-3) - (-1) \times 4\\\\
&|B| = (-15) - (-4)\\\\
&|B| = (-15) + 4 = -11
\end{aligned}Determinant Of $3 \times 3$ Matrix
The determinant of a $ 3 \times 3$ matrix is also possible through cross multiplication; Since we have a larger matrix we need to convert the larger matrix into smaller matrix to compute determinant. See figure below.
Step 1: Select the first row, first element and strike out rest of the elements from first row and first column. Then use to remaining element to create 2 x 2 matrix and find its determinant. See image below.
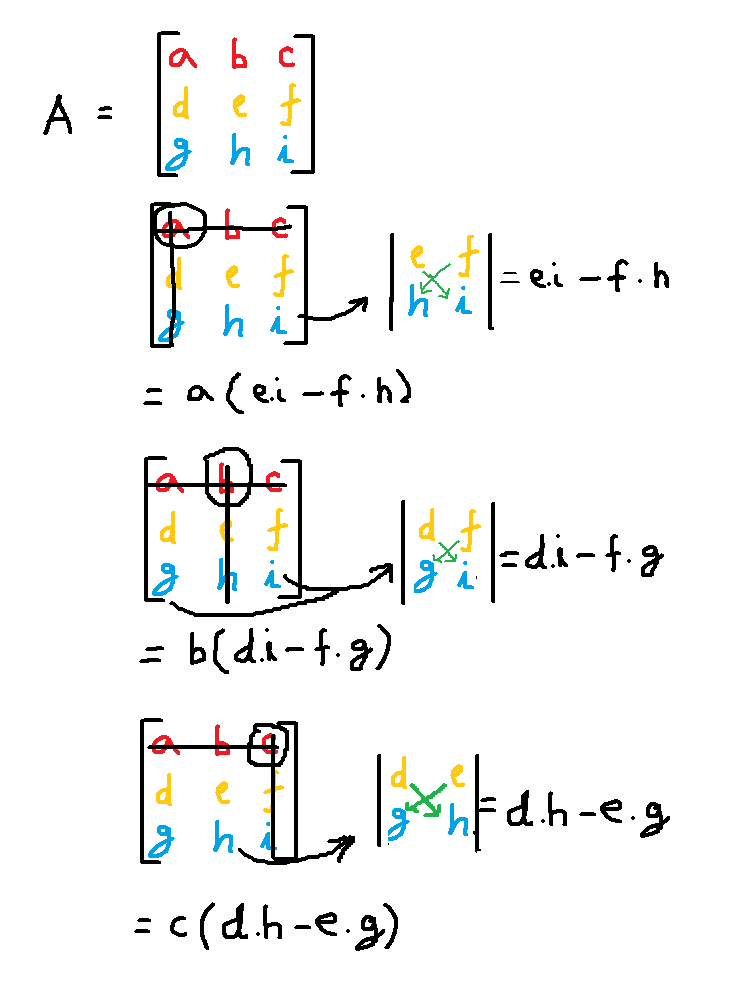
Each selected element must be multiplied with the respective 2 x 2 determinant obtained by eliminating 1st row and the respective column of selected element.
Step 2: Add all terms together and assign a negative or positive sign to each term.
If the selected element from top row (a b c) is $a$. then row $i = 1$ and column $j = 1$. Then the sign of first element
\begin{aligned}
&= (-1)^{i+j}a(ei - fh)\\\\
&= (-1)^{1 + 1}a(ei - fh)\\\\
&= (-1)^{2})a(ei - fh)\\\\
&= +a(ei - fh)\\\\
\end{aligned}Similarly, second element from top row( a b c).
= -b(di - fg)
Third element from top row( a b c).
= +c(dh - eg)
Step 3: Write down the determinant function obtained previously.
The determinant of $3 \times 3$ matrix.
|A| = +a(ei - fh) - b(di - fg) + c(dh - eg)
Let us see few examples of determinant of 
Example #4
Find the determinant of the following $3 \times 3$ matrix.
C = \begin{bmatrix}2 & 1 & 4\\5 & 3 & 7\\2 & 6 & 1\end{bmatrix}Solution:
Given matrix $C$, the determinant is following function.
\begin{aligned}
&C = \begin{bmatrix}2 & 1 & 4\\5 & 3 & 7\\2 & 6 & 1\end{bmatrix}\\\\
&|C| = a_{11}(a_{22}a_{33} - a_{23}a_{32}) - a_{12}(a_{21}a_{33} - a_{23}a_{31}) + a_{13}(a_{21}a_{32} - a_{22}a_{31})
\end{aligned}Therefore,
\begin{aligned}
&|C| = 2(3 \times 1 - 7 \times 6) - 1(5 \times 1 - 7 \times 2) + 4(5 \times 6 - 3 \times 2)\\\\
&|C| = 2(3 - 42) - 1(5 - 14) + 4(30 - 6)\\\\
&|C| = 2(-39) - 1(-9) + 4(24)\\\\
&|C| = 2(-39) - 1(-9) + 4(24) = -78 +9 + 96\\\\
&|C| = 27
\end{aligned}Example #5
Find the determinant of the following $3 \times 3$ matrix below.
A = \begin{bmatrix}-3 & 1 & -6\\2 &-1 & 5\\3 & 9 & 7\end{bmatrix}Solution:‘
Given matrix $3 \times 3$.
A = \begin{bmatrix}-3 & 1 & -6\\2 & -1 & 5\\3 & 9 & 7\end{bmatrix}The determinant is given by following function,
|A| = a_{11}(a_{22}a_{33} - a_{23}a_{32}) - a_{12}(a_{21}a_{33} - a_{23}a_{31}) + a_{13}(a_{21}a_{32} - a_{22}a_{31})Therefore,
\begin{aligned}
&|A| = -3((-1)\times 7 - 5 \times 9)- 1(2 \times 7 - 5 \times 3)+ (-6)(2 \times 9 - (-1)\times 3)\\\\
&|A| = -3((-7) - 45)- 1(14 - 15)+ (-6)(18 - (-3))\\\\
&|A| = -3(-52)+ 1 + (-6)(21) = 156 + 1 -126\\\\
&|A| = 31
\end{aligned}Note that the bigger the matrix , we must find more smaller matrices of size 2 x 2 and its determinant and then add all to get the determinant of original matrix. The process of finding the determinant of smaller matrices and making a matrix of determinants in called matrix of minors.
We shall discuss more about it in the next article.
